An Introduction to the Diels-Alder Reaction

Introduction

The pericyclic reactions are a special category of transformation that involves the concerted, cyclic movement of electrons. There are three broad classes of pericyclic reaction, cycloadditions, electrocyclic reactions, and rearrangements. These reactions demonstrate the predictive power of frontier molecular orbital theory, highlighting the value of visualizing the creation of new bonds at the expense of old ones through the overlap of molecular orbitals rather than the movement of electrons depicted with curly arrows. Having said that, this introduction to the Diels-Alder reaction is going to start at with the basics, and I’ll leave molecular orbitals for another day.

Probably the most studied pericyclic reaction is a cycloaddition known as the Diels-Alder reaction. This powerful reaction creates a six-member ring through the formation of two σ-bonds and one π bond. It can install up to four contiguous or adjacent stereocenters in a highly predictable manner. It is found at the heart of countless syntheses. An example is given below:

An example of the Diels-Alder reaction. This shows a cycloaddition reaction occurring between a diene (purple) and a dienophile (green) to form a new six-membered ring. Two new σ bonds are formed (bold grey lines) and a new π bond (bold purple bond). In this example, three new stereocentres are also created.

The Mechanism of the Diels-Alder Reaction

The Diels-Alder reaction involves the simultaneous reaction of three π (double) bonds to create two new σ (single) bonds and a new π bond. The reaction forms a six-membered ring. The reaction is concerted, meaning all the bonds are made and broken at the same time with no intermediate species formed. This becomes important for the stereochemistry of the reaction. Two examples, highlighting the new bonds formed, are shown below:

Two examples of the Diels-Alder reaction. The new six-membered ring is highlighted as are the three new bonds, two σ bonds and one π bond.

The mechanism of the Diels-Alder reaction is simple, six electrons, represented by three curly arrows, flow in a circle. Each arrow starts from a double bond and finishes on a new bond. It doesn’t matter if the electrons move clockwise or anticlockwise, the product is the same. The reaction is concerted meaning all bonds are made and broken at the same time and there is no intermediate. In other words, the three arrows are always drawn on the same side of a reaction arrow.

The mechanism of the Diels-Alder reaction involves the cyclic movement of six electrons represented with three curly arrows. Each arrow will start from a double bond and it does not matter which direction they flow in.

A transition state showing the electrons spread over the six atoms of the new ring starts to resemble an aromatic ring. This goes some way to explain why these reactions proceed so readily; there is a little of the extra stability found in aromatic rings conferred to the transition state.

The transition state of the Diels-Alder reaction resembles an aromatic ring with a number of π-electrons spread out over six atoms of a ring. This lowers the energy of the transition state and leads to the reaction being more effective.

Cycloadditions, such as the Diels-Alder reaction, are almost the perfect vehicle to introduce frontier molecular orbitals. The overlap of the orbitals helps explain the efficiency of these reactions. The coefficients of the Higest Occupied Molecular Orbital (HOMO) of the diene and those of the Lowest Unoccupied Molecular Orbital (LUMO) of the dienophile match, allowing this combination of orbitals to overlap. This representation, showing the electron rich diene (two π bonds) reacting with the electron poor dienophile (a single π bond) is the version normally shown in organic textbooks. This representation shows the formation of a single bond (most textbooks conveniently fail to mention this as things start to get a little confusing). The second overlap, and the second bond, comes from the LUMO of the diene matching and overlapping with the HOMO of the dienophile. That both combinations is allowable means the reaction progresses well. I've drawn this below. I'm not going to mention the wonders of the Woodward-Hoffmann rules, the conrotatory or disrotatory rotation of bonds, or even whether the reactions are thermally or photochemically allowed (the Diels-Alder reaction is thermally allowed and photochemically disallowed). This is a topic many undergraduates never need (and one I'm very rusty at teaching not having had to cover it myself this century).

The frontier orbital description of the Diels-Alder reaction. This shows that the HOMO of diene can overlap with the LUMO of the dienophile or the LUMO of the diene can overlap with the HOMO dienophile. In fact, both overlaps are important. The orbital approach is powerful but you can understand the reaction without it.

Diels-Alder reaction: Diene and dienophile

There are two components to a Diels-Alder reaction. As drawn below, the first is the diene. This must be contain two, or more, conjugated double bonds. Break the conjugation and the Diels-Alder reaction cannot proceed (other reactions may be possible but that is unimportant in this summary).

The diene is one half of a Diels-Alder reaction. It must be conjugated or the Diels-Alder reaction is impossible.

A second important criterion for the diene is that it must be able to adopt the s-cis conformation. This means the two double bonds must be on the same side of the molecule. You should know that a trans-alkene has two substituents on opposite sides of the double bond and that in a cis-alkene, the substituents are on the same side. The s in s-cis means is we are looking at the conformation of a single bond. Effectively, the s-cis conformation corresponds to the syn-periplanar conformation while the s-trans conformation is the same as the anti-periplanar conformation. All this is easier to see in a diagram.

One the left is the s-trans and s-cis conformation of butadiene. The s-trans conformation is more stable than the s-cis which effectively matches the anti-periplanar conformation of a hydrocarbon. The s-cis conformation is the only conformation that allows conjugated double bonds to act as dienes in the Diels-Alder reaction. This is confirmed when you look at the two cyclic examples on the right. The first is cyclopentadiene, it has the double bonds locked in the s-cis conformation and it is a good diene. The other, 3-methylenecyclohex-1-ene in red, is locked in the s-trans conformation and it can only behave as a dienophile in the Diels-Alder reaction.

The s-trans conformation is normally the more stable conformation but rotation in simple dienes is rapid and has a low energy barrier. Adding bulky substituents to the diene can impede rotation and make the reaction slower or harder to achieve. If the diene cannot adopt the s-cis conformation then it will not participate in a Diels-Alder reaction. In the diagram above, the first cyclic molecule, cyclopentadiene is the two alkenes fixed in the s-cis conformation and it is a very good diene that readily reacts in Diels-Alder reactions. The second cyclic molecule with the external alkene cannot adopt the s-cis conformation and it cannot be a diene in the Diels-Alder reaction. It can react in the Diels-Alder reaction but only as a dienophile (the other component of a Diels-Alder reaction).

The second component of the Diels-Alder reaction is the alkene and it is known as the dienophile as it loves to react with dienes. The dienophile normally contains an alkene conjugated to an electron-withdrawing group (EWG). The diene is considered electron rich due to the four π electrons that are available for reaction. Reactions are invariably more efficient if an electron rich (nucleophilic) reagent reacts with an electron poor (electrophilic) substrate. The dienophile doesn't have to be conjugated to an electron-withdrawing group but ideally one substituent should allow delocalization, for example, styrene (vinylbenzene; PhCH=CH₂) is a good dienophile. The reaction shown in most lectures and textbooks, the reaction of butadiene with ethene, is a rubbish example of Diels-Alder reaction and proceeds with a miserably low yield. The electronics aren't matched; there is no electron deficient coupling partner.

In the Diels-Alder reaction, the dienophile is frequently conjugated to an electron-withdrawing group that activates it. The absence of this group tends to lead to poor reactions that proceed in low yields. The classic example shown at the bottom of the diagram does not give good results with the diene being a better dienophile than ethene.

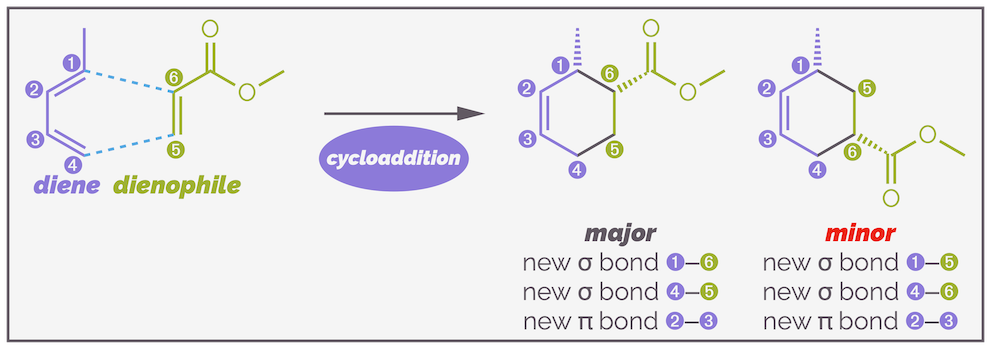
There are common features of the Diels-Alder reaction that should allow you to recognize the product. This is a useful skill if you want to draw the correct product and becomes even more important when (or if) you start to look at retrosynthesis as it will reveal when you can use the Diels-Alder reaction to simplify a synthesis (it is the recognition pattern for the Diels-Alder reaction). First, the Diels-Alder reaction forms a six-membered ring and that ring will contain at least one π bond (alkene). Most examples will have an electron-withdrawing substituent, and this group will be opposite one of the alkenes. Examples are shown below with numbering and color coding as practice.

Examples of the Diels-Alder reaction. The diene is in purple and the dienophile in green. The atoms are numbered to show their origin in the newly formed six-membered ring.

The Regioselectivity of the Diels-Alder reaction

Most examples I have draw so far have involved symmetric dienes and dienophiles, regiochemistry or regioselectivity has not been an issue. But, if you look at the last example in the diagram above, both components are non-symmetric with a single substituent on each. The product shows the substituents next to the each other. Why? And the answer isn't because of how I drew them on the left-hand side! Below is another example, one that highlights the two possible products.

The regiochemistry of the Diels-Alder reaction is predictable. As long as the electronics of the system are matched (there is effectively a nucleophile and an electrophile), the regioselectivity will be high.

The simplest method to predict the regioselectivity is to inspect the polarization of the bonds. If you look at the diene first. The conjugated alkenes allow delocalization of the electrons and it is possible to draw various resonance structures. The most stable of these will position the carbocation on a secondary carbon. This leads to the following polarization of the molecule:

The polarization of the diene can be predicted by inspecting the resonance structures. This provides a simple method to explain the regioselectivity of the Diels-Alder reaction (but there is a caveat to this, which I’ll mention later). I have only drawn the curly arrows for the resonance/delocalization in a single direction (I think this is clearer than having the reverse arrows on the same diagram).

Alternatively, remember that methyl groups (all alkyl groups) are electron donating. This pushes the electrons downwards (in the diagram above), and again shows the same polarization of the diene.

The polarity of the dienophile should be easy to predict (see HERE and HERE). Again, the simplest method is to draw the various resonance structures and determine where the partial charges reside within the resonance hybrid. This is shown below:

The polarization of the dienophile can be predicted by inspecting the resonance structures. This provides a simple method to explain the regioselectivity of the Diels-Alder reaction (but is not the real/accurate reason). For clarity, I have only drawn the curly arrows for the resonance/delocalization in a single direction.

The regioselectivity of the Diels-Alder reaction is predicted by matching the electron rich, partially negatively charged, carbon atoms to the electron poor or partially positively charged centers. In a normal Diels-Alder reaction, the partially negative or nucleophilic carbon of the diene will react with the partially positive or electronegative carbon of the dienophile alkene. The partially negatively charged carbon of the dienophile will form a bond to the partially positively charged atom of the diene. This gives a useful predictive tool that is correct most of the time. An example is below:

The regioselectivity of the Diels-Alder reaction can be predicted by matching the polarization of the two components, the diene and dienophile. The partially negative carbon of the diene will form a new bond to the partially positive carbon of the dienophile and vice-versa.

This simple approach will probably work for all the Diels-Alder reactions that you meet as an undergraduate, and especially those that are said to be electronically matched, with an electron-rich diene and an electron-deficient dienophile. Such systems lead to what is, confusingly, known as the ortho, para selectivity. It is easier to explain this with a diagram (as is the case with most organic chemistry), and this is shown below. When an electron-rich diene with a terminal electron donating group, such as an ether, reacts with an electron-deficient dienophile, such as a acrylate, the major product will have the two substituents adjacent to each other. The reaction proceeds through an aromatic-like transition state in which the substituents are ortho to each other. This gives rise to the name ortho selectivity. I don't particularly like the name (and the idea that there is a pattern to remember instead of a concept to be understood).

The so-called ortho selectivity in the Diels-Alder reaction of a terminally substituted diene. The diagram also shows the similarity between the transition state and an aromatic ring. This explains why some people call these Diels-Alder reactions ortho selective. At the bottom of the scheme is the resonance structures used to determine the polarization of the diene (just as practice). As always, I've only drawn the curly arrows for the resonance structures left to right. This makes the scheme clearer but there is an argument that resonance structures should always been drawn with the arrows showing the movement of electrons in both directions.

Alternatively, if the electron-donating substituent on the diene is at the 2-position, meaning it is on an internal carbon, the favored regiochemistry will be the so-called para product. Here the substituents on each component are on opposite sides of the six-membered ring. The selectivity can be justified with the simple polarization model and matching the most nucleophilic carbon of the diene with the electrophilic 4-position of the dienophile. All of this is highlighted below.

If the electron donating substituent is at the 2-position of the diene the so-called para-selectivity will be observed. An example is shown in the top line. The origin of the name of this selectivity is shown in the second line where the transition state is compared to an aromatic ring. The origin of the selectivity itself can be argued from looking at the polarization of the two components. The resonance structures of the diene is shown at the bottom with only one set of curly arrows. This makes the diagram clearer.

As with so much undergraduate chemistry, the model above, using resonance to determine the polarity of the diene and dienophile, is good for majority of examples. It works well when there is a clear nucleophilic component and an electrophilic component. But, it is a simplification or approximation. Regioselectivity in the Diels-Alder reaction is best explained by matching the atoms of the diene and dienophile so that the carbons with the largest molecular orbital coefficients (the softest atoms or the atomic orbitals that contribute most to the molecular orbital) react. For the example below, the polarization argument, as determined by resonance, gives the wrong product but the molecular orbital description not unsurprisingly predicts the correct product. A discussion of determining the size of the coefficients or even which molecular orbitals are involved in the Diels-Alder reaction is beyond the scope of this summary (which is already too long!).

Using resonance to predict the polarization of bonds and then matching the electron-rich atoms to the electron deficient atoms does not always give the correct result. To truly understand the Diels-Alder reaction you need to look at the orbitals involved. But that is way more complex than you need for at least the first two years of undergraduate.

The regioselectivity of the Diels-Alder reaction can be summarized as below:

The regioselectivity of the ‘normal’ Diels-Alder reaction is summarized above.

The Stereoselectivity of the Diels-Alder reaction

The Diels-Alder reaction reaction is concerted with all the bonds being made and broken at the same time. There are no intermediates in the Diels-Alder reaction with the starting materials being converted to products directly. This means the reaction is stereospecific; the stereochemistry or geometry of the double bonds of the starting materials, the diene and dienophile, is conserved in the product. With the dienophile, a cis-alkene will lead to a syn product while a trans-alkene will give an anti product.

The stereospecificity of the Diels-Alder reaction. The concerted nature of cycloadditions means the stereochemistry or geometry of the alkenes is conserved in the final product. Three different representations for the reaction of a cis and a trans alkene are given. The first is the standard reaction scheme. The second shows the frontier molecular orbital overlap, and indicates that as the bonds are created at the same time the relative stereochemistry between the dienophile substituents must remain the same. Finally, the third representation shows a simple method for determining the relative stereochemistry by overlapping the two components.

The orbital representation is included to show how the two σ bonds are formed as the π bond of the dienophile breaks. This means there is no opportunity for the atoms of the alkene to rotate and the geometry of the alkene is conserved in the relative stereochemistry of the product. Below the orbital representation is a drawing that shows the diene overlapping the dienophile. It places the atoms that will form the new σ bond next to each other. I have bolded the substituents of both the diene and dienophile that will remain together on the same (top) face of the cyclohexene ring in the product. Note how they are next to each other in the representation of the starting materials. This makes it simple (I hope) to determine the relative stereochemistry of the product.

I will get to the reason for drawing the esters under the diene in the cis version soon as it is important for the predictable stereoselectivity of the Diels-Alder reaction.

The geometry of the alkenes in the diene is also preserved in the product. The three representations should indicate the origin of the observed stereospecificity. As all bonds are made and broken simultaneously, there is no opportunity for free rotation of σ bonds and the position of the substituents in the starting materials is reflected in the product. Of the three, I find the bottom, ‘overlapped' representation the easiest to determine relative stereochemistry but the orbital representation is important as it shows the reaction is suprafacial (the orbitals are also useful if you have to use the Woodward-Hoffmann rules and discuss the the disrotatory nature of the reaction).

The stereospecificity of the Diels-Alder reaction. The concerted nature of cycloadditions means the stereochemistry or geometry of the alkenes is conserved in the final product. Three different representations for the reaction of a trans,trans and a cis,trans dienes are given. The first is the standard reaction scheme. The second shows the frontier molecular orbital overlap, and indicates that as the bonds are created at the same time the relative stereochemistry between the dienophile substituents must remain the same. Finally, the third representation shows a simple method for determining the relative stereochemistry by overlapping the two components.

The concerted nature of the reaction means it is stereospecific, but the Diels-Alder reaction is also stereoselective. The diene and dienophile can approach with two different orientations and this leads to two different diastereomers. The two possibilities are the endo and exo products as shown in the example below:

The Diels-Alder reaction is stereoselective. There are two orientations the diene and dienophile can approach each other and this leads to the endo and the exo product. While the exo product looks more stable, with less steric interactions between the coupling partners, the endo is normally preferred.

In the majority of examples, the endo product is favored. At first glance, this looks counterintuitive, the endo product is more sterically congested and the transition state has the diene and dienophile overlapping, maximizing their steric interactions. The exo product looks more attractive. The dienophile is on the ‘outside', pointing away from the rest of the molecule. The exo product is more stable. It is the thermodynamic product but the Diels-Alder reaction is invariably under kinetic control. This means the product that forms faster is favored.

The endo product is favored as the transition state is stabilized by ‘secondary orbital interactions’. It is suggested that there is a stabilizing interaction between the electron-deficient LUMO of the carbonyl group of the dienophile and the electron-rich HOMO of the diene if the dienophile can sit under the diene. To simplify the drawing, I have shown this with an acrylate rather than the lactone above.

The endo selectivity of the Diels-Alder reaction arises due to secondary orbital interactions. There is a stabilizing overlap of the HOMO of the diene with the LUMO of the carbonyl of the activated dienophile in the transition state that leads to the endo product that is absent in the transition state of the exo product pathway.

The existence of secondary orbital interactions is still argued in the literature even though it has become ‘fact’ or ‘canon’ in undergraduate textbooks. There is a review that indicates there is no conclusive evidence to support secondary orbital interactions HERE (Acc. Chem. Res. 2000, 33, 658; https://doi.org/10.1021/ar0000152) but there are still many supporters of this hypothesis with much information backing up the claim (find reference to Houk’s calculations).

That the endo product is the kinetic product and the exo is the thermodynamic product can be seen from reversible Diels-Alder reactions. The classic example of this is the reaction of furan shown below. This leads to the exo product as this is more stable. The exo product suffers from less internal steric interactions. The reaction is reversible due to the aromatic characteristics of furan. Furan fulfils the criteria of aromaticity but, due to the electronegativity of oxygen, it is relatively less aromatic than benzene. It can react as a diene (non-aromatic characteristics), but there is a degree of aromatic stability and the reaction will go in the opposite direction to reform the furan ring.

The Diels-Alder reaction of furan is a reversible reaction. This leads to the more thermodynamically stable, exo product, being favored over the normally observed exo product. The reversibility is due to the aromatic characteristics of furan.

The stereochemistry of the Diels-Alder reaction can be summarized in the following diagram. It is not an accurate representation of the transition state, but it does act as a workable model for predicting the outcome of these important reactions. The key is that an electron-withdrawing group or conjugated substituent on the dienophile favours the endo product and will be ‘under' the diene in the transition state. Using the overlapping representation, substituents on each substrate that face in the same direction, bolded in the diagram, will be on the same face of the cyclohexene.

The relative stereochemistry of the Diels-Alder reaction is easy to predict if you draw the reactants correctly. An electron-withdrawing group or conjugated substituent on the dienophile will sit under the diene to maximize secondary orbital interactions. Once you have this correct, the substituents closest to each other will be on the same face of cyclohexene product.

Summary of the Diels-Alder reaction

The Diels-Alder reaction involves coupling a conjugated diene with a dienophile, one that is normally activated by an electron-withdrawing group, to give a substituted cyclohexene ring. During the reaction, two σ bonds are formed at the expense of two π bonds. It is the archetypal pericyclic reaction, and is classed as a cycloaddition. This means it proceeds through a concerted mechanism with no intermediate. It is stereospecific in terms of the geometry of the double bonds and is stereoselective when looking at the approach of the two reactants. Invariably, the endo product is favored. All this means that up to four contiguous (adjacent) stereocenters can be formed with high predictability. This adds up to a powerful reaction that has been used in a host of syntheses.

A summary of the Diels-Alder reaction showing how the regioselectivity and stereoselectivity can be predicted from two normal examples in which the dienophile is electron-deficient and the diene electron-rich.

This has only been the briefest introduction to the Diels-Alder reaction. I haven’t discussed the use of Lewis acids or organocatalysts to accelerate the reaction. I haven’t talked about the control of absolute stereochemistry through substrate control, the use of chiral auxiliaries or asymmetric catalysis. I’ve only alluded to the importance of orbitals in the Diels-Alder reaction and the wonderful world of the Woodward-Hoffmann rules.

The Diels-Alder reaction is even more powerful than mentioned in this introduction as it can create many different flavors of six-membered ring. There are intramolecular Diels-Alder (IMDA) reactions, where the diene and dienophile are connected in the same molecule. These lead to bicyclic molecules (top example below). There are inverse electron demand Diels-Alder (iEDDA) reactions, where the electronics have been swapped and the dienophile is electron-rich while the diene is electron-poor. This transformation (middle of the scheme below) comes with a bonus version of the Diels-Alder reaction, after the initial cyclization, there is a retro-Diels-Alder reaction, an elimination that gives the final heterocycle. Additionally, there are hetero-Diels-Alder reactions in which one, or more, atoms have been replaced with a heteroatom. The latter permits the formation of heterocycles. An example of each of these is given below:

The Diels-Alder reaction is versatile. The basic principles covered in this summary can be applied to the synthesis of different cyclic molecules. The top row shows an intramolecular Diels-Alder reaction (IMDA) that leads to the formation of a bicyclic system. The middle example is very interesting, it is both an inverse electron demand Diels-Alder reaction (iEDDA), meaning that while the components are still electronically matched, the diene is now electron-deficient and the dienophile is electron-rich. It is also an example of a hetero-Diels-Alder reaction, with one of the carbon atoms of the diene replaced by a nitrogen atom. The middle row also shows a retro-Diels-Alder reaction, an elimination that breaks a six-membered ring and gives a pyridine along with nitrogen gas. The final row shows another hetero-Diels-Alder reaction (HDA). Here an electron-rich diene attacks an aldehyde as the dienophile and leads to a pyran system.

Pericyclic Reactions

The Diels-Alder reaction is the prototypical example of a cycloaddition, one of a family of reactions that make up pericyclic reactions. Diels-Alder reactions are known as (4+2) cycloadditions or [4+2] cycloadditions. This ridiculous distinction is based on whether you are counting (atoms) or [electrons]. There are other types of cycloaddition, such as dipolar cycloadditions, which are examples of (3+2)-cycloadditions that lead to the formation of five-membered rings. They are still [4+2]-cycloadditions! The 1,3-dipolar cycloaddition of an azide with an alkyne to give a triazole is, erroneously, known as the 'click reaction' (in reality, it is just an example of a 'click reaction’). This cycloaddition is either a (3+2) cycloaddition as it involves three atoms from the azide and two from the alkyne or is a [4+2]-cycloaddition as it involves four electrons on the azide or dipole and two on the dipolarophile or alkyne.

Another example of a cycloaddition reaction. This is a 1,3-dipolar cycloaddition or (3+2)-cycloaddition or [4+2]-cycloaddition depending on how you want to classify it.

Other pericyclic reactions include electrocyclic reactions where one π bond is swapped for a σ bond, as in the following example:

An example of an electrocyclic reaction.

Rearrangements can also be pericyclic reactions. Here the number of σ and π bonds does not change and you effectively isomerize a compound. An example is the Ireland-Claisen reaction of silyl ketene acetals:

An example of a rearrangement reaction. This is an example of the Ireland-Claisen rearrangement.

Eventually, I might write a summary on other cycloadditions and some of the rearrangements but it is very unlikely that I’ll cover the electrocyclic reactions.