An Introduction to Chirality
Introduction
Let's clear one thing up from the start, chirality is not a chemical concept, it is based on the geometry or shape of an object. The world can be divided into two sets of objects, those that are chiral and those that are achiral. Most students seem to think that chirality is something special. I’d argue that it isn’t, most objects, especially if they have writing on them, are chiral, and it is achiral objects that are in the minority. So what is chirality?
An object is chiral if it is non-identical to its mirror image while an achiral object is identical to its mirror image. Hands are chiral (if you ignore fingerprints and scars), with you left hand being a non-identical mirror image of the right hand (in fact, the word chiral is derived from the Greek for ‘hand’). Most people intuitively know that left and right-handed objects are different, and what is true of ‘real world’ objects is equally true of chemistry and molecules. This is why you often hear chemists talk about left and right-handed molecules when talking about chiral compounds. The inherent difference between the left and right hands is why chirality is important.
Below there is a cartoon of hands as an example of chiral objects and a sphere, such as a snooker ball, as an achiral object due to it being identical to its mirror image.
Chiral and achiral objects.
Chiral versus Achiral
What exactly do we mean when we say chiral objects are non-identical mirror images? Isn’t the whole point of a mirror that it gives you a perfect reflection of the original object? Not quite. When discussing chirality, being non-identical mirror images means the original object and its reflection cannot be superposed or they cannot occupy exactly the same space.
Your hands are chiral because the left and right hands are mirror images that cannot occupy the same space. You could presses your hands so that your fingers and thumbs match up (like the prayer gesture or 🙏) but you can see the knuckles of both hands, they are not occupying the same space. Alternatively, overlap your hands so that both sets of knuckles face up. Your hands are still not superposed,* the thumbs are pointing in different directions. Your hands are chiral.
*As an aside, most books have it wrong! They say that chiral objects are non-superimposable. This is incorrect. Superimposable means to overlap or place on top (normally so that both objects are still visible). Superpose means to overlap so that all parts coincide. This imprecision is really frustrating (almost as frustrating as the fact I still say superimposable even though I know it is wrong).
An achiral object can be superposed or is identical to its mirror image. The ball in the example above is achiral as it can be superposed so that it occupies the same volume.
The more technical definition of chirality is based on symmetry. Chiral objects cannot have any element of symmetry except for an axis of rotation (another way of putting this is that chiral objects cannot have any reflective symmetry elements). That last clause is important. It explains why chiral does not necessarily mean asymmetric (a very successful class of chiral ligand are the bis(oxazolines) or BOX ligands. These are chiral but they are also symmetric, they have a C2 rotational axis (you can spin them through a 180° and they look the same)).
It is hard to draw three dimensional shapes in two dimensions and even harder to convince the viewer that they are the same or different. I’ve tried and I hope some of you find these pictures useful.
Chiral objects are not identical to their mirror image. Chiral objects cannot have a plane of symmetry, inversion center or axis of improper rotation (wow that got technical fast).
Achiral objects will have some form of symmetry (in addition to an axis of rotation), they are symmetric. Often you will see it stated that chiral objects will not have a plane of symmetry (also known as a mirror plane), while achiral objects will have a plane of symmetry. This isn’t true, but is rather a generalization as a plane of symmetry is the most important or common form of symmetry but it is not the only form. Achiral objects might have a center of inversion or a rotation/reflection axis (axis of improper rotation).
An achiral object is identical to its mirror image. It will have either a plane of symmetry, an inversion center or a rotation/reflection axis. The above example has two planes of symmetry shown in red.
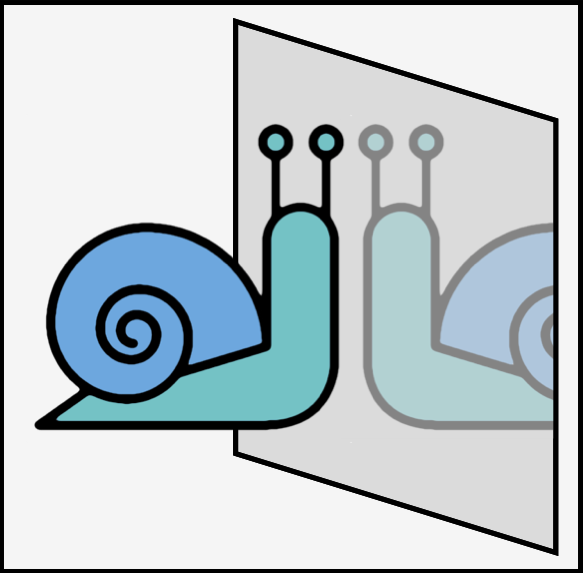
Examples of chiral objects includes hands, gloves, feet, shoes, propellers, corkscrews, golf clubs, snail shells and the horns of certain sheep. Such objects have no symmetry (see above for the exception) as exemplified by the cartoon snail below. Achiral objects (if they have no writing one them) include balls (these have an infinite number of planes of symmetry), tennis rackets (without writing), nails (as in, hammer and nails), and most cutlery (but not fish knifes!). Most cutlery has a plane of symmetry as shown in the diagram below. In my drawing forks and spoons having a vertical plane of symmetry running through the center while the knife has a horizontal plane (this is the same as if you had set a table normally).
A snail is chiral due to the helix of the shell. The shell has no symmetry. If you are really interested, something like 90% of all snails are right-handed helices although this number is both species and population dependent.
Cutlery (ignoring hallmarks & other engravings) are achiral. The fork and spoon have a plane of symmetry coming vertically out of the plane of the picture while the knife, as drawn, has a plane of symmetry parallel to the picture.
Building an Understanding of Chirality
Over the years, I have found that some students just get chirality. They understand why our hands are mirror images but are different and, more importantly, they can apply that understanding to the more abstract idea of a three-dimensional shape or a molecule. Others can't. They cannot picture how one tetrahedral atom can be achiral while another can have 'handedness' simply by changing a single group on it. Throwing students in at the deep end with three-dimensional chirality can be daunting. Some students find it useful to start in one-dimension and work up to three dimensional objects.*
*I’m not the only person who has spotted this, but, more importantly, I’m not the first to write about it using the examples below … honestly, I thought I’d come up with this myself but it is so eerily similar to the earlier paper referenced here J. Chem. Ed. 2005, 82, 1009, that I suspect that I have unconsciously rephrased it (I own Robert Gawley’s book on asymmetric synthesis so I clearly like his explanations). Luckily, I spotted this before publishing this blog and can reference it as a source!
Chirality in one-dimension.
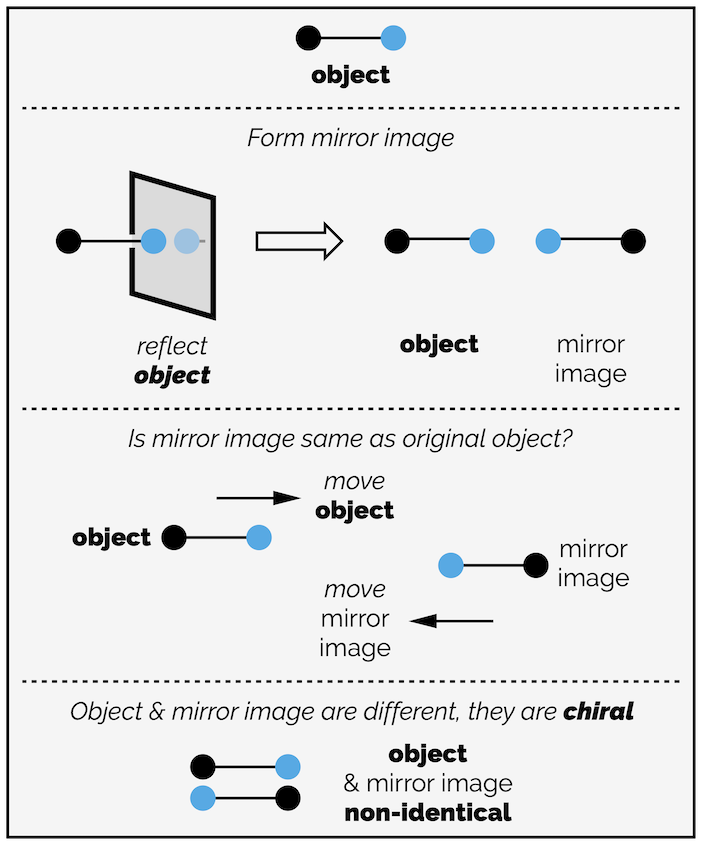
A line is a one-dimensional object. In the diagram below, that dimension is left-right (the x axis). The object can only move in one-dimension, it can only move left and right. If you start with a line with a black dot at either end, it will be achiral. It will be identical to its mirror image (technically, the mirror should be a mirror point as we’re in one dimension but I’ve drawn mirror to emphasize the action).
An achiral object in one dimension. The point of reflection should also be in one dimension so should be a point of reflection but to make it easier to see (but technically incorrect) I have drawn a mirror.
Now change one of the dots to a color. The object is now chiral (in one dimension), it is no longer the same as its reflection. The two lines cannot overlap (remember you can only move the line left or right and cannot rotate it, that would be a second dimension) so that the color dots are in the same place.
A one-dimensional chiral object.
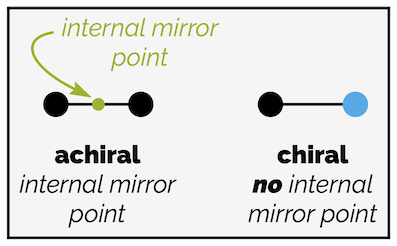
The first line has a point of symmetry (an internal mirror point) and is achiral. The line with two different ends has no internal mirror point and is chiral.
An achiral object will have an element of symmetry. Chiral objects don't (when we're looking at more dimensions that can have rotational symmetry but no elements with reflective symmetry.
Chirality in two dimensions
To make a two dimensional object, add a third dot and form a triangle. This now occupies both the x and y axes. This object is allowed to move in two dimensions. It can move anywhere in the plane of the page, which means it can move from side to side, up and down or rotate (anti-)clockwise. It cannot flip over as this would involve the third dimension or the z axis.
An achiral object in two dimensions. Now rotations are allowed but no flips. Again, I shouldn’t have drawn a 3D mirror and the reflection should take place along a mirror line (as we are in two dimensions).
The triangle with three black dots is clearly achiral. Its mirror image is identical to the original object (the reflection should be along a mirror line and not the three dimensional mirror I have drawn but again, I’m doing this to stress what I have done and not to be mathematically correct). What happens of you replace one dot with a colored dot? The object is still achiral. Rotating the reflection allows the mirror image to coincide with the original triangle as shown below.
An equilatoral triangle with two different colored corners is still achiral. Simple rotation of the reflection (which should have occurred along a line of reflection not a plane as drawn) allows the two objects to coincide.
If you add a third dot of a different color the triangle is finally chiral (in two dimensions). Now the mirror image is different. It cannot coincide with the original object no matter how many times you move or rotate it (remember, in two dimensions you cannot flip the object).
A triangle with three different corners is chiral. It is impossible to move the reflection (yes,it should have been reflected along a line) of triangle in two dimensions so that all the corners match with the original triangle.
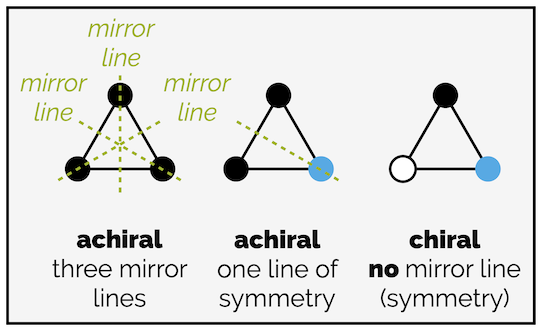
A (equilateral) triangle with three identical corners has three lines of symmetry (three internal mirror lines) and is achiral. A triangle with two different corners has one line of symmetry and is still achiral. With three different corners, there is no symmetry (in two dimensions) and the triangle is chiral.
Achiral objects will have at least one mirror line in two dimensions. Chiral objects have no line of symmetry in two dimensions.
For someone of my age, a classic example of chirality in two dimensions (it is only in the x and y axes) is Tetris. This game allows movement only in the plane of the screen, either from side-to-side, downwards (up-down but, annoyingly never up) or rotation but no flipping. The latter is important as it means the pieces can be divided into those that are achiral (I, O & T) and have at least one line of symmetry, and those that are chiral (J, L, S & Z), which have no symmetry.
Tetris tiles can be split into achiral and chiral tiles. ‘I’, ‘O’ and ‘T’ are achiral as they have at least one internal line of symmetry (shown as a mirror above).
I’ll use Tetris to show you why chirality is important a little later (but if you have ever played Tetris, you already know the reason).
Chirality in three-dimensions
By adding a point, a vertex, attached to the three corners of the triangle you create the three dimensional shape called a tetrahedron (like chemists don’t know what a tetrahedron is). Finally, we can use all three axes, x, y and z, and movement is now possible in all three dimensions. The shape can be translated (moved), rotated or flipped. At this point, I hope that you can see that if all the corners are the same color, the shape will be achiral and will have multiple internal mirror planes or a planes of symmetry. The same is true if there are two different colored corners and even three different colors. To remove all planes of symmetry requires four different corners as shown below.
Chirality in three dimensions.
I hope that by building from one dimension to three, it is clear why undergraduate courses are obsessed with four different substituents on an sp3 or tetrahedral atom. But I must repeat my initial comment from the introduction, having four different groups on a tetrahedron is not the reason why molecules are chiral. Shape (and the symmetry of that shape) is the only important thing. Can the original object be superposed on its mirror image or not?
Why is Chirality Important?
Intuitively you already know the answer to this question, just think about putting your shoes on in the morning. You left foot only fits in the left shoe (comfortably). This is the result of chirality.
An achiral object and its mirror image are identical. They will interact with other objects in an identical manner. This should come as no surprise, as I said, they are identical. There is no difference between a person catching a ball or catching its mirror image. All the properties are the same. You can think of the reverse as well. There is no difference in holding a ball in your left or right hand. All the properties are the same.
The interaction between either mirror image of an achiral object and a chiral object is the same.
The interaction between either mirror image of a chiral object and an achiral object is the same.
Replacing the ball with a glove changes everything. Instead of an achiral object interacting with your hands, there is a second chiral object. Now it matters which mirror image of the glove you have. Only the left glove will fit on your left hand. The mirror image glove, the right-hand glove will not. Two chiral objects have different interactions depending on the mirror image involved.
The mirror images of chiral objects behave differently in the presence of other chiral objects. Mirror images are different.
An alternative example is the interaction between a nut and a bolt. If you have a bolt with a clockwise thread you can only attach or thread a nut with an identical clockwise thread. If you take the mirror image of the bolt, it will have an anti-clockwise thread. It will not fit in the original nut.
Nuts and bolts are chiral. The two mirror images of a bolt are different and only one will interact (screw into) a nut.
The two paragraphs below and the diagram below are attempts to sum this key point up (I probably should have edited this out of the summary but the picture looks so nice (and took me so long) that I want an excuse to keep it in!):
Achiral objects will have the same interaction with either mirror image of a second object (regardless as to whether the second object was chiral or not). But chiral objects interact differently with each of the mirror images of a second chiral object.
So the key to this summary is that the mirror images of achiral objects are identical and will behave the same whatever they interact with. Mirror images of chiral objects are almost identical but behave differently when they interact with other chiral objects (or things).
The two mirror images of an achiral object will have the same interactions with a chiral object. The resulting combined objects will be mirror images as a result of the original chiral object. The interaction of two mirror images of a chiral object with a second chiral object will be different. The resulting adducts will be different, they will not be mirror images. The interactions of chiral objects with chiral objects is different.
If the analogy of your feet interacting with shoes, or nuts and bolts, doesn’t convince you that chiral objects behave differently with other chiral objects then I can try again with something a little more fun and return to our discussion of Tetris. Earlier you saw that the Tetris pieces can be divided in two; those that have a mirror line and are achiral, I, O and T and those that have no symmetry and are chiral, J, L, S & Z. If you are playing a game of Tetris and you are given a ’T’ piece it will fit on the board below.
An achiral ’T’ piece and its mirror image both fit in the gap (and complete the line). This is no surprise as the mirror image of an achiral object is identical to the object.
The mirror image of the ’T’ piece is another ’T’ piece and it fits equally well (of course, it does, it is the same. It doesn’t matter that the board, in this case, is chiral (it is not the same as its mirror image).
The frustration of Tetris arises when the game keeps giving you ’S’ pieces which will not fit into this chiral board. You need the mirror image, the ‘Z’ piece if you want to complete the two lines. The ’S’ and ‘Z’ pieces are mirror images but they don't behave the same. They are chiral. They have different interactions with other chiral pieces, such as the board.
The ’S’ piece is chiral. It is different to its mirror image, the ‘Z’ piece. Only one of the two mirror images will fit into the slot in this chiral board.
Chirality and Chemistry
Molecules behave in exactly the same way as other objects, and are either achiral or chiral. Achiral molecules have an identical mirror image while chiral molecules are non-identical to their mirror image.
Achiral and chiral molecules have the same properties as achiral and chiral objects.
Chiral molecules and their mirror images are stereoisomers. Stereoisomers are a class of isomer meaning they have all the same atoms but these atoms are arranged differently. Stereoisomers have all the same atoms and all the same bonds, they have same constitution, but they are different due to their shape which means they are non-superposable or cannot occupy the same space. Two non-identical mirror images are known as enantiomers. Two stereoisomers that are not mirror images are known as diastereomers. I have written a summary of stereoisomers HERE.
Chiral molecules are a type of stereoisomer. Non-identical mirror images are called enantiomers while non-mirror image stereoisomers are called diastereomers.
As chirality is the result of a physical property (shape) and not a chemical characteristic, all the statements above about chiral and achiral objects also apply to molecules. Chiral molecules cannot have an element of symmetry other than a possible axis of rotation. In other words, achiral molecules will have one, or more of the following, a plane of symmetry (mirror plane), a center of inversion or an axis of improper rotation (rotation/reflection). Fortunately, the plane of symmetry is most common as this is easier to see than the other forms of symmetry.
The diagram below shows an achiral molecule, isopropyl alcohol, with the internal plane of symmetry cutting through the hydroxyl group and bisecting two methyl groups. It then shows that adding a methyl group to one side to give butan-2-ol breaks the internal plane of symmetry and results in butan-2-ol being chiral. Finally, there is an example of a bis(oxazoline). This is chiral. It has no plane of symmetry, no center of inversion, and no improper rotation, but it is not asymmetric. It does have an axis of rotation. And for those of you that like symmetry, it is C2 symmetric.
Achiral molecules will have at least one other element of symmetry beyond an axis of rotation. Most commonly, this is a plane of symmetry. Chiral molecules, at most, have an axis of rotation or no symmetry at all.
One property of molecules makes them more complicated (until you ignore it … which you will at undergraduate). Molecules are not static and there is constant rotation around single bonds, or the molecules are said to be changing conformation. This leads to even the simplest molecules, such as ethane, existing as non-superposable mirror images in the majority of their potential conformations. Should we consider these molecules as chiral? No. A good way to think about chirality is through the concept of residual stereoisomers. Residual stereoisomers are the shapes of molecules that can be distinguished by a given analytical technique. For example, proton NMR cannot differentiate the different conformations of ethane so they are not stereoisomers. 1H NMR can differentiate the geometry of certain amides, and so they can be said to exist as E or Z isomers even though C–N bond rotation is possible. In practice, this means you can consider any molecule that has at least one accessible symmetric conformation as achiral, or if the static representation of a molecule (its drawing) is achiral then the molecule is considered achiral.*
*Yeah, I know, this is a simplification and I’m ignoring compounds like atropisomers (restricted rotation) for the time being. Let’s try and keep the introduction simple!
A single molecule can be chiral but a substance, or a collection of molecules, cannot (a collection of molecule is unlikely to be a mirror image). A collection of chiral molecules will have one of three compositions: It can be enantiomerically pure meaning it consists of a single mirror image of the compound. It can be enantiomerically enriched if it contains more of one mirror image than the other or it can be a racemate or racemic mixture, which means it contains an equal quantity of the two enantiomers.
Molecules can be chiral, substances made up of chiral molecules are either enantiomerically pure, enantiomerically enriched or racemic.
The properties of the two enantiomers of a molecule are almost identical. This is to be expected, they are mirror images of each other. They will have the same physical properties in terms of boiling point, melting point, infrared spectra, NMR etc. The two enantiomers will only differ when they interact with another chiral species.
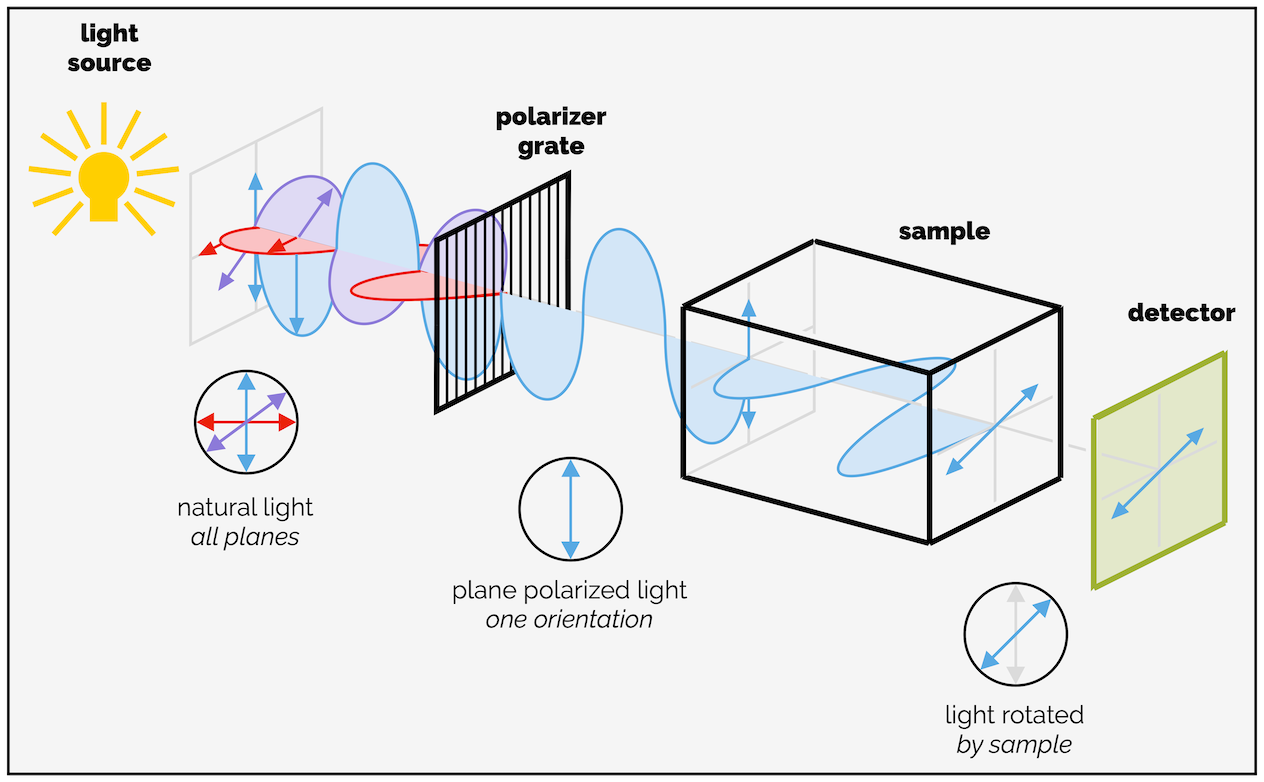
There are two major upshots from this. The first is that the two enantiomers rotate plane polarized light in opposite directions. This gives rise to what is known as optical rotation.* For most undergraduates, it is sufficient to know that a pure enantiomer rotates plane polarized light by a certain number of degrees in one direction. The mirror image will rotate plane polarized light the same amount but in the opposite direction. The size of the rotation is proportional to the purity of the same so that an enantiomerically enriched sample that contains 75% of one enantiomer and 25% of the other will rotate light by 50% the amount of a pure sample (25% is cancelled out by the other enantiomer or is effectively a racemic mixture). A racemic mixture or a 50:50 mixture of enantiomers does not rotate plane polarized light as each enantiomer cancels out the action of the other.
*If you are lucky, I might one day write a summary on this subject alone (somewhere I already have a diagram showing the helical path of the electric field component of light).
Cartoon of a polarimeter and the rotation of plane polarized light by an enantiomerically pure compound.
If you know how much a pure enantiomer rotates plane polarized light you can determine the purity of a mixture by measuring the size of the optical rotation/specific rotation.
The second important consequence is that chiral molecules can react differently with other chiral molecules. The most obvious example of this is the interaction of chiral molecules with biological systems. The machinery that controls living organisms, enzymes, are composed of amino acids. All bar one of the amino acids are chiral (the exception is glycine, which is achiral). This means that enzymes are chiral and that the two mirror images of a chiral molecule may have different interactions with the enzyme. This leads to enantiomers having different properties. The examples below show some of the surprising differences that can be found between enantiomers.
Different enantiomers can have different biological activities. R & S describes the stereochemistry in the molecule. A detailed explanation can be found in a previous summary HERE.
An overlooked consequence of enantiomers becoming different in the presence of other chiral molecules is that a sample of an enantiomerically pure compound does not necessarily have the same physical properties as a sample containing a mixture of enantiomers. For instance, an enantiomerically pure sample of tartaric acid has a melting point of 172 °C but the racemic mixture (both mirror images) melts at 206 °C. Why is the ‘same’ compound behaving differently? In a pure sample, there is only one mirror image. In a racemic mixture, there is a second chiral molecule, one enantiomer can interact with itself or a different chiral molecule, their mirror image and this allows different intermolecular interactions.
Enantiomerically pure substances can have different properties to mixtures of enantiomers of the same compound.
Chirality and Stereocenters
At undergraduate level, chiral compounds are normally identified by the presence of a stereogenic center, also know as a stereocenter or, far too frequently, chiral center (I'm not a fan of this term due to the confusion it causes when we have meso-compounds. How can an achiral compound have two, or more, chiral centers? It just seems wrong). In this context, a stereocenter is a tetrahedral atom with four different groups or substituents coming off it. But, please be aware that molecules without a stereocenter can be chiral and molecules with multiple stereocenters can be achiral. The only real definition of a chiral molecule is that it cannot be superposed upon its mirror image (or a compound lacking any form of symmetry other than a rotational axis).
It should be clear from the discussion of chiral objects above why a tetrahedral atom requires four different groups to be considered a stereocenter but below is a diagram that again shows that four different groups is a necessity to remove any plane of symmetry. If all the vertices are the same there are multiple planes of symmetry. If there are two different vertices there are at least two planes of symmetry (this would be two white circles and two blue circles) or three planes of symmetry for the molecule shown. With three different vertices, there is a single plane of symmetry. It is only with four different corners that we break the symmetry.*
*it should be noted that this paragraph is only correct if none of the groups coming off the central tetrahedral carbon are connected to one another. As soon as the molecule contains a ring all bets are off!
A cartoon showing that there must be four different groups coming off a tetrahedral atom for it to be a stereocenter and be chiral.
While it is a useful skill to be able to identify stereogenic centers within a molecule (identify tetrahedral atoms with four different groups), I must stress that this is not the same as identifying a chiral molecule. A molecule with a single stereogenic center will be chiral but a molecule with multiple stereogenic centers might not be chiral. With multiple stereoentres, it becomes possible for the molecule to have an element of symmetry and hence be achiral. Molecules that contain stereogenic centers but are achiral are called meso compounds. The classic example is tartaric acid.
Some molecules with multiple stereogenic centers are still achiral. These are known as meso compounds.
“Other” Chiral Molecules
A molecule is either chiral or it is not. It is chiral if the shape or geometry of the molecule results in a lack of certain symmetry elements. But, chemists like to think in terms of bonds, and this means we often classify chiral molecules by the stereochemical element that breaks the symmetry. Or, in English, we we use stereochemistry/stereoisomers to categorize different “kinds” of chirality (this annoys many people). All this means is that the absence or presence of a stereogenic centre, a tetrahedral atom with four different groups coming off it is not a necessity for chirality.
In this introduction to chirality I don’t want to go into detail about the “other” kinds of chirality (the other stereochemical motifs that break the symmetry of a molecule), but I do want to show examples of these molecules so that you are aware of their existence (this is also the reason I spent most of this summary not discussing molecules). Below are chiral molecules that do not have a stereogenic center but are chiral. If you are interested I have published various posts on how chemists name or give a stereochemical descriptor to so-called planar chirality, axial chirality or helical chirality.
Chiral molecules that do not contain a stereogenic center.
Conclusion
There are two kinds of object, those that are chiral and those that are achiral. Achiral objects are identical to their mirror image. The mirror images are the same thing. Chiral objects are not the same as their mirror image. The object and its reflection are said to be non-superposable as they cannot occupy the same volume of space. Achiral objects include balls, spoons and chairs (as long as there is no writing on any of these objects). Chiral objects include shoes, gloves, and screws. Basically, anything that can be described as either left- or right-handed, is chiral. The properties of the pair of chiral objects will be almost identical - they are mirror images so they are identical in almost every way. Two chiral objects will only differ in one way, how they interact with another chiral object. Think about your left shoe. This is identical to your right shoe (or at least it was when you bought it) except it will only fit on your left foot. It is different when it interacts with your chiral foot.
Molecules are exactly the same, they are either chiral or achiral. If they are achiral then they are identical to their mirror image. If they are chiral then the molecule and its mirror image will be non-identical. They are said to be non-superposable. The chiral molecule and its mirror image are known as enantiomers. A molecule is chiral if it has no element of symmetry (it can have a rotational axis but it cannot have a plane of symmetry, a center of inversion, or an improper rotation axis (rotation and reflection). Achiral molecules will have symmetry above and beyond an axis of rotation. The most common form of symmetry is a internal plane of symmetry.
A molecule can be chiral but a substance or collection of molecules cannot. A substance comprising of chiral molecules will be enantiomerically pure if only contains one enantiomer. It will be enantiomerically enriched if it is predominantly one enantiomer but is contaminated with the mirror image. If there is an equal quantity of both enantiomers it is called a racemic mixture.
As enantiomers are mirror images they are almost identical. All their physical properties, such as melting point or solubility will be the same as will their reactions with achiral reagents. The only difference between the two enantiomers occurs when they interact with another chiral species. This means each enantiomer will rotate plane polarized light in opposite directions. It also means that enantiomers can have different interactions with biological systems such as our bodies.
Chirality is a fascinating topic and this is just a simple introduction.