Diastereoselective addition to aldehydes & ketones
Introduction
Nucleophilic addition to an aldehyde or ketone can create a new stereocenter in a molecule. A flat, sp2 hybridized carbon is transformed into a tetrahedral sp3 carbon atom. If the four substituents are different then the atom is a stereocenter.
Addition to a carbonyl group can create a new stereocenter depending on the substituents and the nucleophile.
If the aldehyde or ketone already contains a stereocenter, the reaction results in the formation of diastereoisomers, and there is an opportunity for substrate control. This means the substrate influences which diastereotopic face of the carbonyl is attacked by the nucleophile. In other words, it can control the proportion of each diastereoisomer formed.
In this summary, I shall introduce the most common models for predicting or rationalizing the stereochemical outcome of addition to an aldehyde or ketone with an α-stereocenter. The nucleophile will be achiral.
This summary introduces the different models for predicting or rationalizing which diastereotopic face of a chiral aldehyde or ketone is preferentially attacked by an achiral nucleophile.
The importance of the products of this reaction mean that there is wealth of literature studying stereoselective addition to aldehydes and ketones. The models rationalizing our observations have evolved in terms of complexity. It is clear, that there isn’t a single universal explanation and that selectivity is controlled by every chemists favorite cliché, “a complex combination of steric and electronic factors.” More detailed discussion can be found in: Chem. Rev. 1999, 99, 1191 or J. Am. Chem. Soc. 2006, 9433 and any number of books on asymmetric synthesis (my favorite (until I write my own … almost a joke if it wasn’t for the 600 pages on my computer) being “Principles of Asymmetric Synthesis” by Gawley & Aubé).
Addition to the carbonyl group
To understand the stereoselectivity it is necessary to consider the conformation of the electrophile and the angle of attack of the nucleophile on the double bond. Both factors influence the interactions between reactants and control which face is attacked.
The angle of attack, or the trajectory the nucleophile approaches the carbonyl group, determines which parts of the electrophile are going to interact with the nucleophile. Two angles are important, the Bürghi-Dunitz angle and the Flippin-Lodge angle.
The Bürgi-Dunitz angle is based on the observation that nucleophiles approach the carbonyl bond along a trajectory of approximately 107° (often quoted as 105 ± 5°). This arises through the maximization of the overlap of the highest occupied molecular orbital (HOMO) of the nucleophile with the lowest unoccupied molecular orbital of the carbonyl group, which is the π* antibonding orbital. The LUMO is distorted due to a node running through the center and points roughly along the Bürgi-Dunitz trajectory. A second argument that is often quoted is that this angle of attack minimizes disfavored electrostatic interactions between the nucleophile’s HOMO and the full π bonding orbital.
The Bürgi-Dunitz angle is based on the observation that nucleophiles approach the carbonyl group at an obtuse angle of approximately 107°. The separation of nucleophile and oxygen atom is maintained throughout the reaction.
The separation of the electron rich nucleophile and the electron rich oxygen atom (it has two lone pairs of electrons at the start of the reaqction and three by the end) is maintained throughout the addition. As the carbon changes hybridization from trigonal planar sp2 to tetrahedral sp3 there is minimal change in the angle separating the substituents. This is important as it allows us to assume that the transition state resembles the product more than the starting carbonyl compound (hence in most of the diagrams below I will draw both the Newman projection of the starting material and a more sawhorse like diagram. The former are normally used to predict the product, the latter are probably a better representation).
The key upshot of the Bürgi-Dunitz trajectory is that the nucleophile passes over the substituents R and R2 of the carbonyl compound. This means a stereocenter on these substituents can influence which face of the carbonyl group is attacked.
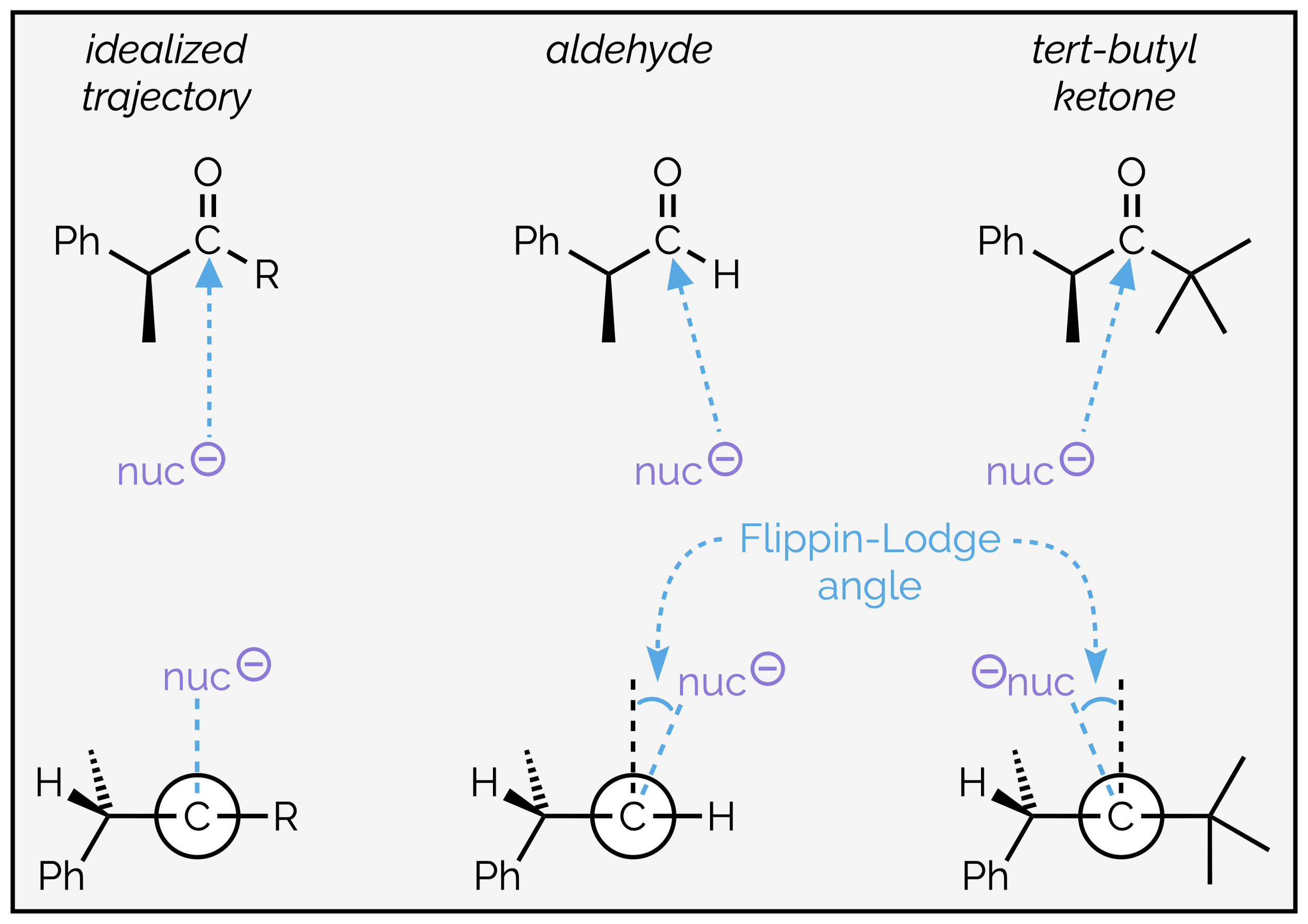
The Bürgi-Dunitz trajectory assumes the nucleophile bisects R and R2 with the nucleophile approaching perpendicular to both substituents. This is unlikely to be true, and the Flippin-Lodge angle is a measure of the deviation from the idealized approach. In aldehydes, the nucleophile is thought to approach the carbonyl group by a pathway that is closer to the small, sterically insignificant hydrogen atom. This reduces the non-bonding interactions with stereocenter of the second substituent and can lead to reduced diastereoselectivity. A bulky ketone can force the approaching nucleophile closer to the stereocenter and increasing the selectivity.
The Flippin-Lodge angle describes the deviation of the nucleophiles approach from the idealized 90° to the carbonyl group. It is influenced by the substituents on the carbonyl group.
The lowest energy conformation of an aldehyde or ketone, the so-called ground state conformation, is eclipsed with the largest substituent aligned with the C=O double bond (exactly how we normally draw our line diagrams … there is a reason why we draw them as we do). Calculations suggest that torsional strain, the barrier to rotation caused by the repulsion of electrons in a bond, is more important in the transition state than it is in the ground state. This means the transition state is closer to the conformation of the product than the starting materials and will be staggered. Combining this with the Bürgi-Dunitz trajectory means that a good representation for the approach of the nucleophile is given in the diagram below.
Representing the trajectory of the approaching nucleophile.
In the diagram above, I have drawn the substituent anti to the incoming nucleophile. There is thought to be some degree of stablization of the forming bond by hyperconjugation, overlap of the σ bonding and σ* antibonding orbitals, and this can only occur if the new bond and the existing bond are parallel. This effect is often ignored to give the simplified representation below, which is found in many undergraduate textbooks:
The standard representation for a nucleophile approaching along the Bürgi-Dunitz trajectory.
The nucleophile
Most discussions of diastereoselective addition of nucleophiles to aldehydes and ketones ignore the nucleophile. I'll be doing the same very soon, but before I do I just want to say that this is a gross simplification. The nature of the nucleophile makes a big difference to the selectivity even if it is achiral.
In this summary, I'll be discussing additions involving what can be termed σ-transfer nucleophiles. Such reagents use a σ bond or lone pair of electrons to attack the carbonyl group. I will not be discussing π-transfer nucleophiles, which are either allylic nucleophiles or enolates. The transition states of the two different classes of reagents can be very different, with the former normally readily simplified to a spherical anionic nucleophile.
Nucleophiles that involve a nucleophilic σ bond or lone pair of electrons will be covered in this summary. Those that involve a nucleophilic double bond will not.
For the vast majority of this summary, I will be considering all nucleophiles to be simple anions attacking the carbonyl group. Obviously, this is incorrect but it is a good starting point. Nucleophiles are invariably far more complex. Organoboranes frequently do not follow the models presented in this summary. The reason for this is that the bulk of these reagents is not aligned with the Bürgi-Dunitz trajectory as shown below:
Most organic chemists are happy to simplify nucleophiles to an anion, R–. This is what I'll be doing for the rest of the summary. It misses both the beauty of the real structures and can lead to mistakes (as in the case of organoborane reducing reagents).
Organometallic reagents often attack through a cyclic transition state, such as that shown for the Grignard reagent above. This makes them more complex (pun intended) than considered in the summary below, but, for the most part, they still follow the predicted reaction outcomes.
Felkin-Anh Model
The first model most students meet is the Felkin-Anh model. This predicts which diastereoisomer will be favored when a nucleophile attacks an aldehyde or ketone with a stereocenter in the α position, and it is largely based on steric hindrance. If a substituent on the stereocenter is highly polarized, a different model is used.
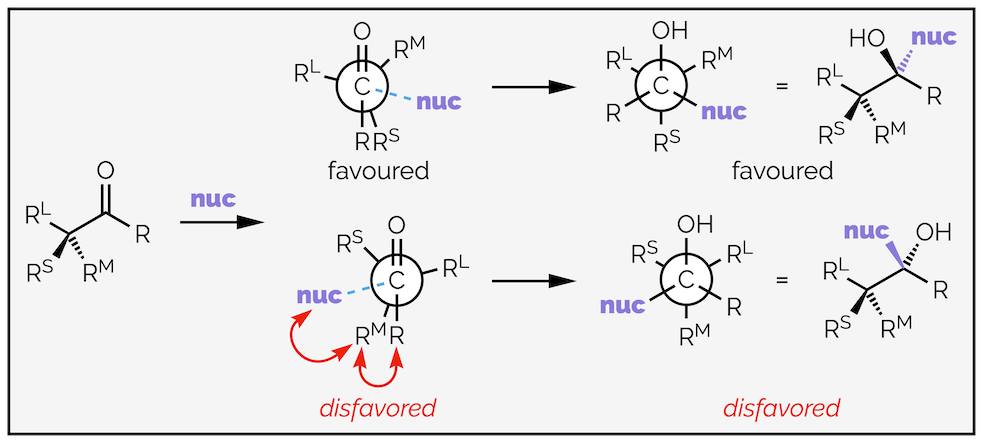
In its simplest form, the Felkin-Anh model assumes that the largest substituent will be perpendicular to the carbonyl group. This gives two conformations. The favored product is formed by the nucleophile attacking along the Bürgi-Dunitz trajectory and passing the smallest of the remaining substituents on the stereocenter. All other approaches are disfavored due to non-bonding interactions with larger substituents.
The Felkin-Anh model of stereochemical addition to chiral aldehydes and ketones is based on minimizing non-bonding interactions between the incoming nucleophile and the substituents of the α-stereocenter.
The model above has been refined so that the largest substituent is anti to the incoming nucleophile, and not perpendicular to the carbonyl group, as this offers further stabilization to the transition state as discussed in the previous section. As the model is based on steric interactions between the nucleophile and the electrophile, the size of the nucleophile will have an effect. The larger each reactant becomes the more selective the reaction as shown below:
Reduction of the chiral ketone is diastereoselective. The bigger the reductant the greater the selectivity.
A simplified generalization of the Felkin-Anh model is given below. The nucleophile will approach along the Bürgi-Dunitz trajectory. The largest substituent (RL) on the α-stereocenter is anti to the incoming nucleophile. Of the two possible conformations that match these criteria, the favored reaction occurs with the nucleophile passing close to the smallest substituent (RS), while the disfavored conformation has the medium substituent (R) disrupting this trajectory. The more observant will note that there is a potential interaction between the substituent on the opposite side of the carbonyl and the medium substituent, this is one of the arguments for the increased selectivity observed with bulky ketones. The other argument is that bulky ketones will influence the Flippin-Lodge angle.
General diagram representing the Felkin-Anh model of stereoselective addition to aldehydes or ketones with an α-stereocenter.
The Felkin-Anh model can predict which diastereoisomer will be favored but it cannot predict the degree of selectivity. This is especially true when you remember that the nature of the nucleophile plays an important role. Both examples above add a hydride to the carbonyl group. In both cases the Felkin-Anh model would predict the correct stereochemical outcome but it would not tell you that Selectride gives the higher selectivity as the Felkin-Anh model does not take into account the size of the nucleophile.
Polar Felkin-Anh Model
The selectivity of certain additions cannot be explained using the steric arguments of the Felkin-Anh model and it is necessary to consider electronic factors as well. The following reduction is diastereoselective for the anti-Felkin-Anh product if you assume that the methyl group is larger than the chlorine atom. You can make this assumption! If you inspect the barriers to rotation in substituted cyclohexane derivatives, you find that there is a larger barrier to rotation for methylcyclohexane, which has a value of 7.1 kJ mol–1 while chlorocyclohexane has a value of 1.8 kJ mol–1 suggesting it is smaller and easier to flip into the axial position.
Reduction of the ketone above favors the anti-Felkin-Anh product.
The selectivity can be explained by if the most electronegative substituent is anti to the incoming nucleophile, and this is the basis to the polar Felkin-Anh model. This conformation permits hyperconjugation or delocalization of the π* antibonding orbital into the σ* antibonding orbital of the electronegative substituent. The more electronegative the substituent the greater the delocalization and the the lower the LUMO of the carbonyl. This leads to a favored reaction.
Hyperconjugation or delocalization of the π* C=O and σ* C–Cl orbitals leads to stabilization of the conformation with the most electronegative group anti to the incoming nucleophile.
The polar Felkin-Anh model, or electronic model, can be generalized as shown in the scheme below. Here Z represents an electronegative group.
General diagram representing the polar Felkin-Anh model of stereoselective addition to aldehydes or ketones with an electronegative group, Z, on the α-stereocenter.
It is impossible to take the two models in complete isolation, and it is almost certain that steric factors will still influence the polar Felkin-Anh model.
Modified Cornforth Model
There is still considerable debate as to the validity of the polar Felkin-Anh model. As I started my independent career working in the lab opposite Sir John 'Kappa' Cornforth's lab, and quickly learnt to listen to his advice, the other electronic model I’m going to give is the modified Cornforth model. This model works well for a number of troublesome examples.
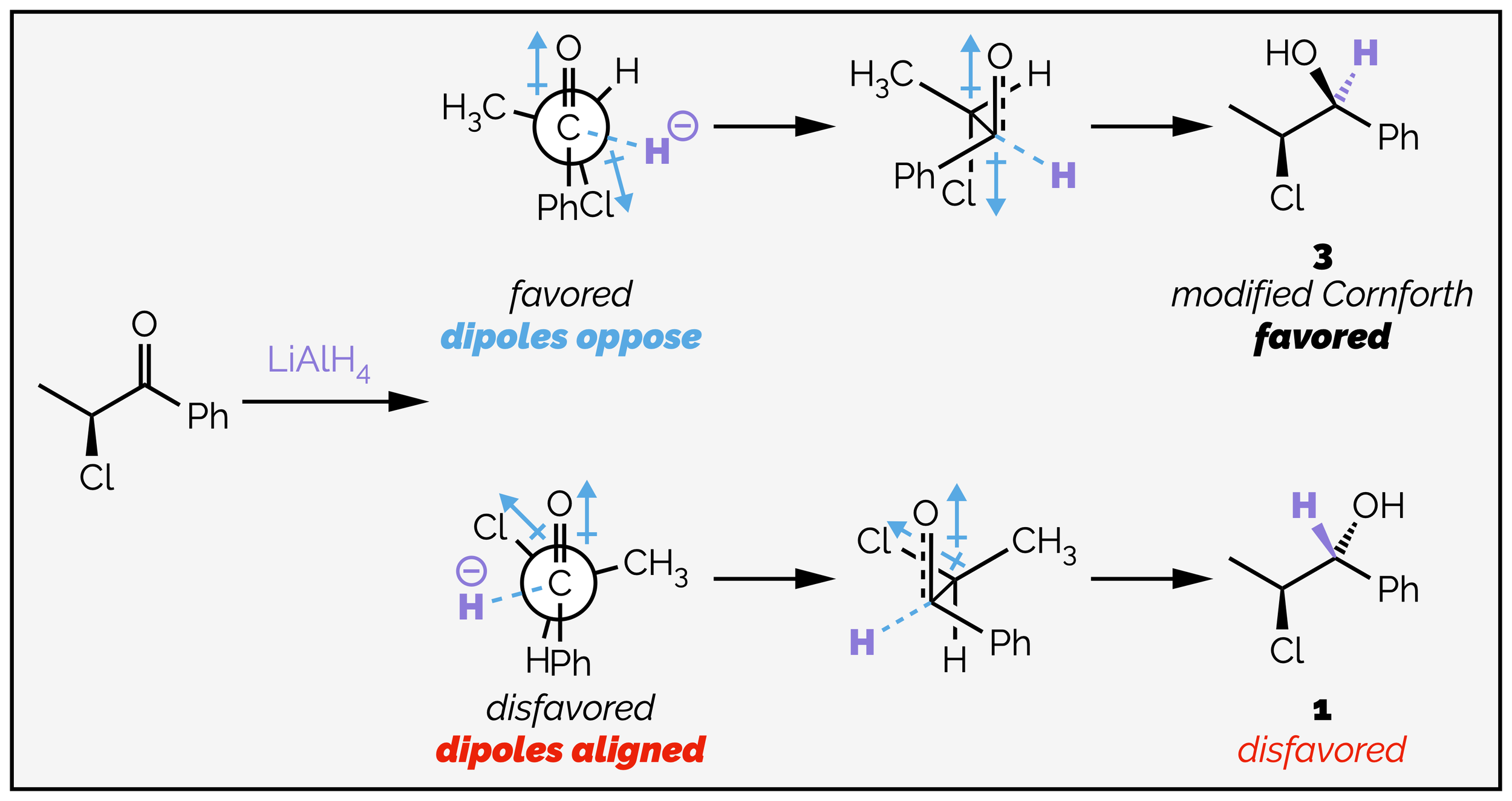
The Cornforth model was based on electrostatic interactions and the minimization of the dipole in the transition state. This means the the dipole of the carbonyl group and the electronegative substituent should oppose each other. The modern modification of the Cornforth model is to include the trajectory of the nucleophile along the Bürgi-Dunitz angle along with having the a substituent of the stereocentre anti to the nucleophile. This is shown for the chloro derivative seen earlier.
The reduction of a ketone with an electronegative α-substituent. The diastereoselectivity can be rationalized by the modified Cornforth model.
Normally, the modified Cornforth model predicts the same outcome as the polar Felkin-Anh model but it is not without its problems. In the example above, the top transition state (the favored transition state) has increased torsional strain with the phenyl and chlorine atoms being almost eclipsed. This cannot be good. On the other-hand, the disfavored transition state minimizes this interaction, having a proton eclipsing the phenyl but, gives the wrong product. The advantage of the modified Cornforth model is that it can correctly rationalize a number of troublesome examples, including the organoborane-mediated reduction below:
The modified Cornforth model correctly predicts the outcome of the organoborane-mediated reduction while the polar Felkin-Anh model would give the wrong answer.
Organoborane reductions occur by through a different mechanism to hydride reductants. The boron interacts with the carbonyl group directly so that an intermediate boronic ester is formed after nucleophilic addition. The upshot of this is that the bulk of the organoborane is closer to the oxygen of the carbonyl group and not positioned along the Bürgi-Dunitz trajectory. By minimizing the dipoles, the modified Cornforth model leads to a transition state with the small hydrogen atom hindering the approach of the reductant. Such a transition state is favored and correctly predicts the major diastereomer. To minimize steric interactions between the reactants, the polar Felkin-Anh model, with the electronegative substituent anti to the incoming nucleophile, would predict attacking occurring from the opposite face of the carbonyl group. This gives the minor diastereomer. This suggests the modified Cornforth model has some merit.
A generalization is given below:
The modified Cornforth model is based on the minimization of electrostatic effects (minimize the dipoles of the electronegative substituent and the carbonyl group or the incipient alkoxide).
In most examples, both the polar Felkin-Anh and the Cornforth model give the same prediction.
Cram Chelation Control
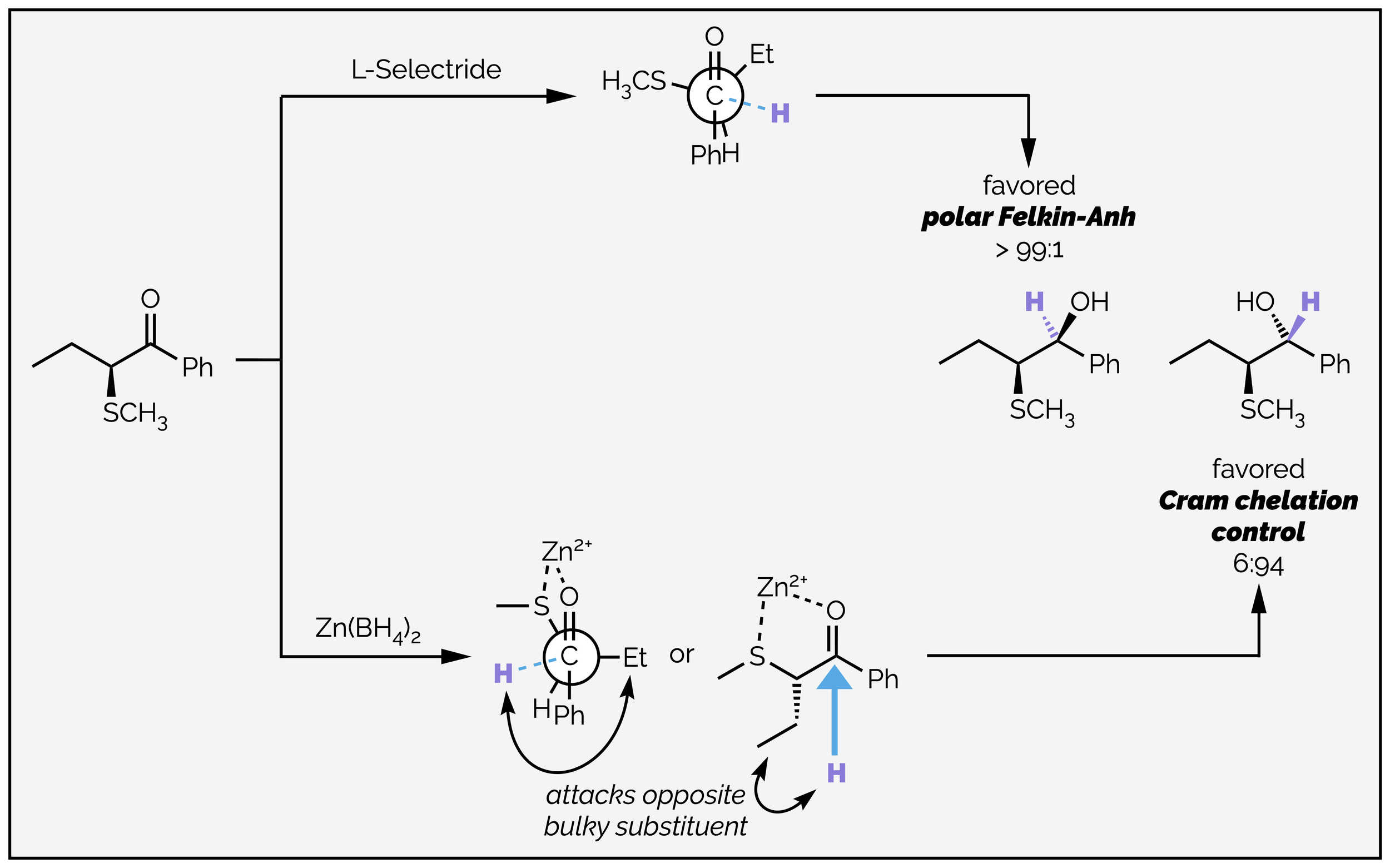
If there is a Lewis basic substituent on the α-stereocentre then chelation is possible and the conformation of the carbonyl substrate can be fixed in a rigid, cyclic structure. This can allow reversal of the normal selectivity. The difference chelation can make is shown in the reduction of the sulfide below. Use of L-Selectride leads to the expected product as predicted by the polar Felkin-Anh model. The electronegative sulfur is anti to the incoming nucleophile, which preferentially attacks in the conformation that has the hydrogen hindering approach along the Bürgi-Dunitz trajectory.
Chelation can reverse the normal selectivity of a reaction by restricting the conformation of the substrate. This is known as Cram chelation control.
When zinc borohydride is the reductant, the diastereoselectivity is reversed. The zinc coordinates to the sulfur and the carbonyl group, effectively locking to the two Lewis basic groups in an eclipsed conformation. The nucleophile then attacks the least sterically demanding face. This new model is known as Cram chelation control.
The structure of the substrate can determine whether Cram chelation control is possible. The second example shows reduction of two ketones. When there is an acetal protecting group, chelation of the weakly Lewis acidic lithium cation is possible and the reaction occurs through the Cram chelation model. If a bulky silyl ether protecting is used, chelation is no longer possible and the diastereoselectivity is best rationalized with the polar Felkin-Anh model.
The diastereoselectivity of the reduction can be reversed depending on the protecting group. The silyl ether prevents chelation and the stereoselectivity is rationalized with the polar Felkin-Anh model. With an acetal protecting group, chelation is possible and Cram chelation control predicts the product outcome.
The Cram chelation control model can be generalized in the diagram below:
A generalization of the Cram chelation model, where Z is a Lewis base (has a lone pair of electrons).
Evans Reduction
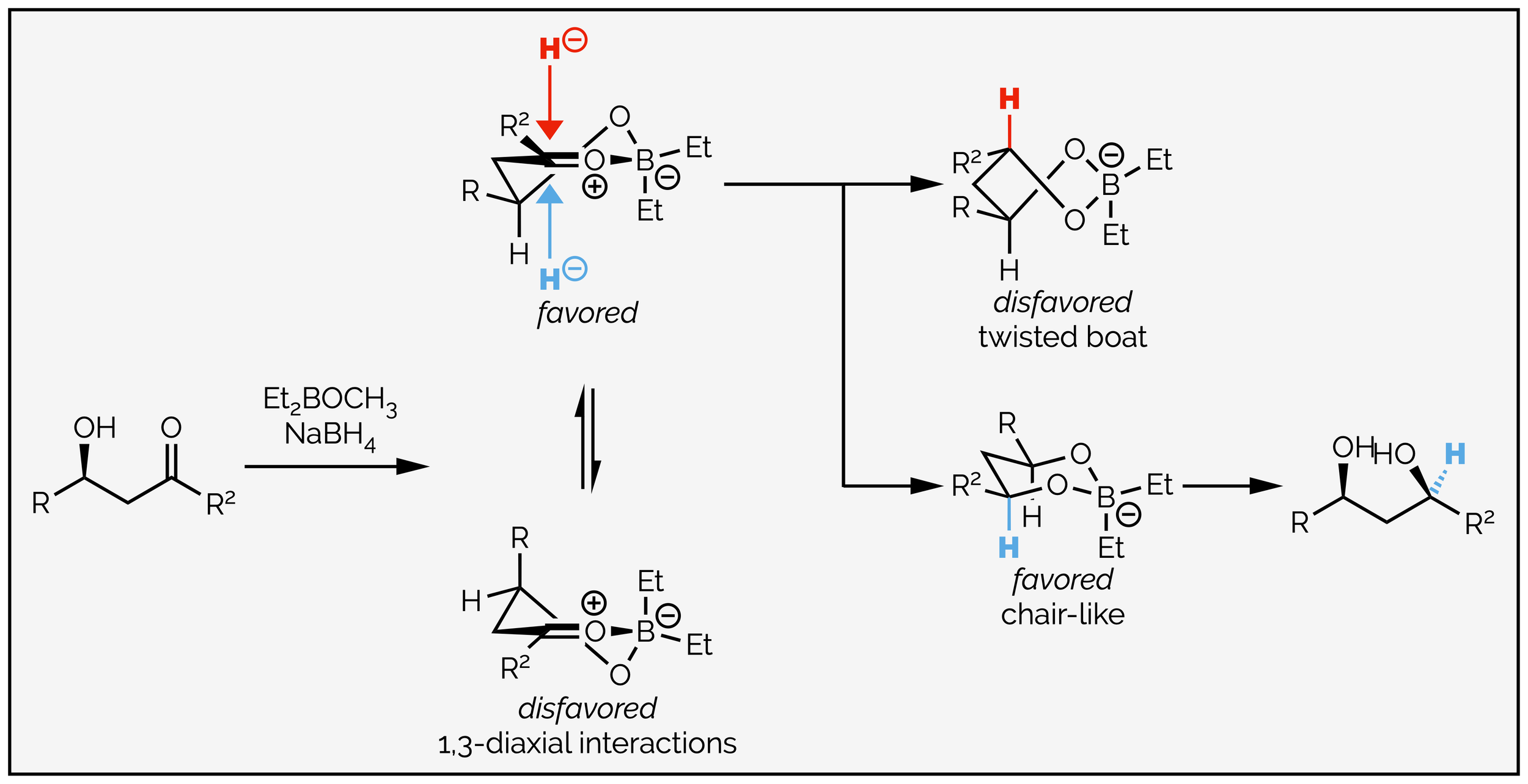
The last stereoselective addition to a ketone that I want to discuss are the two Evans-directed reductions of β-hydroxyketones. This useful methodology shows how you can combine different models to predict the stereochemical outcome of reductions. Or by changing the reagents you can selectively access either diastereoisomer. The reduction is slightly different to the previous reactions in that it is an example of 1,3-stereochemical induction. This means the stereocenter is in the β-position. The two reactions are:
Choice of reactant permits both diastereoisomers to be formed selectively.
The difference between the two reductions is chelation. The reduction on the left, forming the 1,3-syn diol is formed by the boron reagent tying the alcohol and ketone together so that a six-membered chelate is formed. Reduction occurs by intermolecular delivery of the hydride. The diastereoselectivity can be understood by inspecting the half-chair conformation. The simplest explanation states that the favored conformation has the substituents in the pseudo-equatorial position to minimize 1,3-diaxial interactions. The nucleophile approaches from the axial position, opposite the ring substituents. Axial approach leads to a favored chair-like transition state, while approach from the other face of the carbonyl would give a high energy twisted boat conformation.
The 1,3-syn product is formed when a Lewis acid that can tie the carbonyl and β-alcohol together. The chelate sits in a conformation that places the substituents pseudo-equatorial, and the nucleophile approaches in an intermolecular fashion to give the chair-like intermediate, not the twisted boat intermediate.
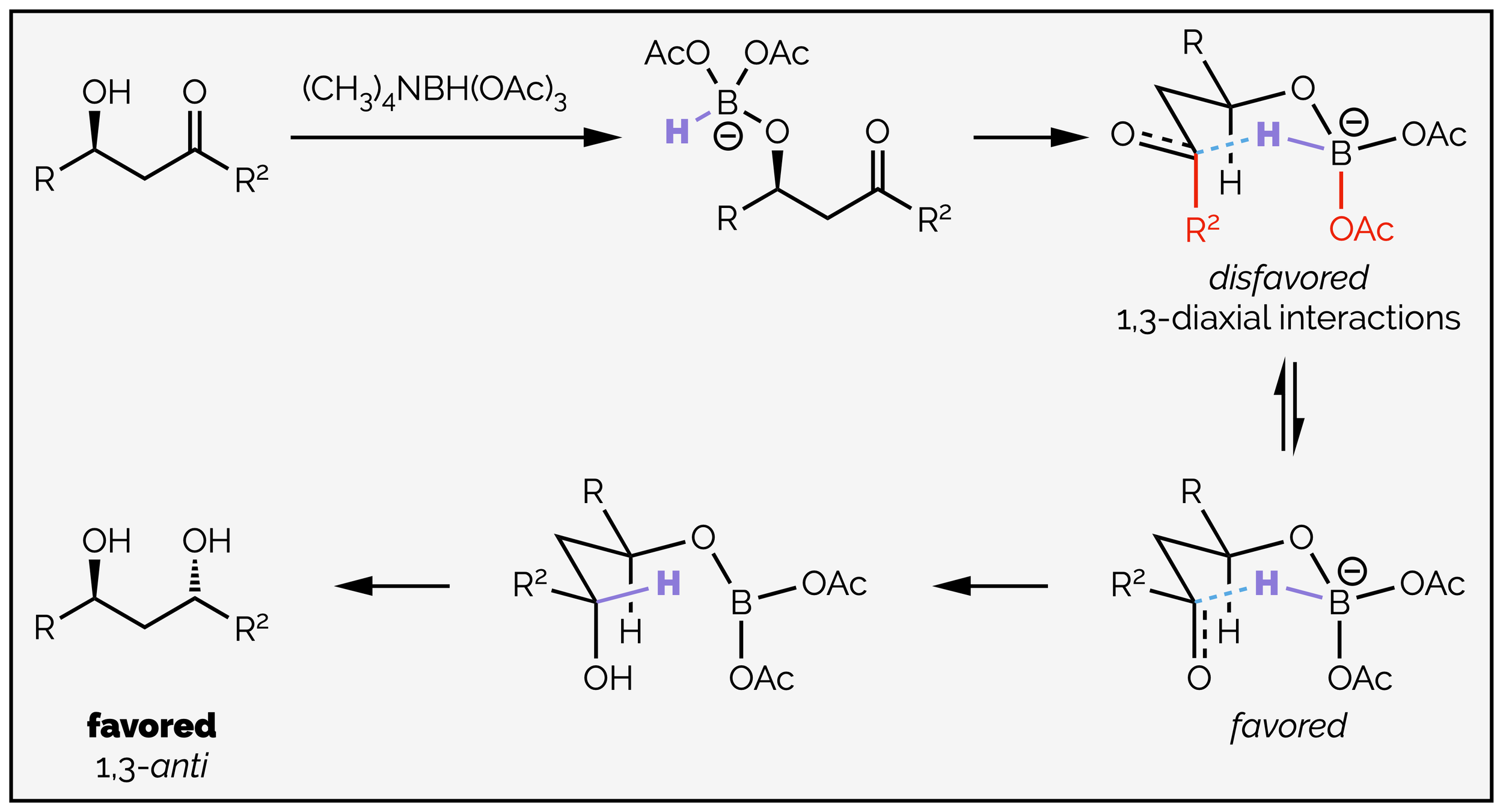
The 1,3-anti diol is formed when there is intramolecular addition of the hydride. This occurs when tri(acetoxy) borohydride is used as the reductant. This reagent must be activated by interaction with an alcohol prior to reaction. This means the first step is substitution of an acetoxy group to give the tethered reductant joined to the rest of the molecule. The adduct can deliver the hydride through a six-membered transition state that adopts a chair-like conformation. The favored transition state has the largest group pseudo-equatorial. The carbonyl group is pseudo-axial so that the ketone substituent is in the pseudo-equatorial position. The hydride is delivered along the Bürgi-Dunitz trajectory to give the 1,3-anti diol.
The 1,3-anti product is formed when the reaction is intramolecular, with internal delivery of a hydride through a chair-like transition state.
Conclusion
This summary gives a brief introduction to substrate control in the addition of nucleophiles to aldehydes and ketones. I have only given broad brush strokes of simple examples with either an α or β-stereocentre. You need to realize that both steric and electronic effects influence the selectivity. The nature of nucleophile has a large effect on the stereoselectivity. The models above are simple and work for nucleophiles that can be approximated to anions. There are numerous examples that do not agree with these models, and as a result there are many other models.
Hopefully, this is a useful summary for undergraduates and postgraduates early in their careers.
A brief summary of the most common models for diastereoselective nucleophilic addition to aldehydes or ketones.