An Introduction to the Conformation of Cyclohexane
Introduction
Cyclic molecules are important throughout Nature. They are more rigid than acyclic or linear molecules as the bonds have less freedom to rotate. Because of this, rings can provide a framework from which to hang useful functionality. Cyclohexane holds a special place in the undergraduate study of saturated (no multiple bonds) cyclic molecules. It is the least strained of the cycloalkanes and has a well-defined conformer. What is often glossed over is that all the principles that apply to cyclohexane apply to other six-membered rings as long as the ring atoms are sp3 hybridized. This means the shape of cyclohexane can be applied to sugars and alkaloids. In fact, the principles covered here are often used to describe the transition states of reactions involving six atoms as anyone who has studied the aldol reaction will know.
In this summary, I will cover the basics of cyclohexane, including how to draw the favored conformer of cyclohexane, place substituents on the ring and then determine which conformation is favored.
Before looking at cyclohexane, let’s see why it holds such a special place in chemists’ hearts.
Ring Strain
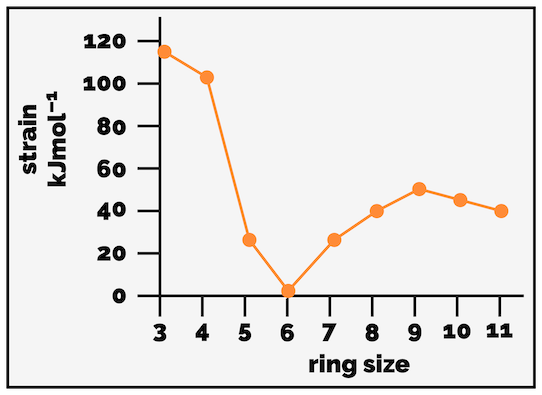
The strain in a cyclic molecule can be plotted against ring size and it looks roughly like that graph below (apologies, I made this in ChemDraw and not Excel … its the trends I want not the precise values).
Strain in cycloalkanes.
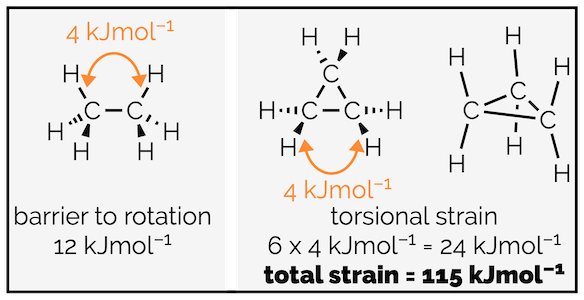
The large strain energy for the small rings (cyclopropane and cyclobutane) cannot be explained by torsional and steric strain alone. By looking at the barrier to rotation in ethane it is possible to estimate a value for the torsional strain caused by the overlap of C–H bonds (12 kJmol-1 is caused by three pairs of C–H bonds are eclipsed so each on contributes 4 kJmol-1). This only accounts for 24 kJmol-1 (six pairs of C–H bonds) of cyclopropane’s approximately 115 kJmol-1 of strain.
Torsional strain in ethane and one component of the strain in cyclopropane.
The remaining 91 kJmol-1 of strain is largely attributed to ring or angle strain (although some of this remaining strain must be torsional strain from the eclipsing C–C bonds). Each of the cycloalkanes comprises of a ring of tetrahedral sp3 carbon atoms that want to have a bond angle of 109.5°. The internal angles of a triangle, like cyclopropane, are 60° while a square, as our drawing of cyclobutane shows, would be 90°. Ring or angle strain develops as the sp3 centres are forced to have these non-ideal bond angles.
Cyclopropane - forcing a tetrahedron into a triangle.
Strain in cycloalkanes is a balancing act between torsional and ring strain. Both cyclobutane and cyclopentane increase their ring strain so that they can decrease torsional strain. Both could adopt planar shapes that have bond angles closer to 109.5° (cyclobutane as a square would be 90° and cyclopentane as a pentagon would be 108°) but have puckered shapes to reduce torsional strain. Cyclobutane is butterfly shaped (bond angle 88°) and cyclopentane is envelop shape (bond angle 105°).
Cyclobutane and cyclopentane reduce torsional strain at the expense of ring or angle strain.
As the plot above shows, cyclopentane and cyclohexane have little strain, this is why they are common motifs within nature. Cyclohexane is considered strain free, which might explain why it is so important.
Cyclohexane
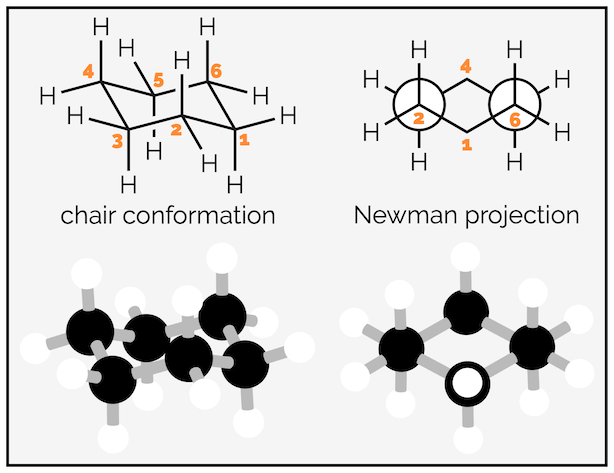
Cyclohexane can adopt two conformations that are free of ring or angle strain, the chair and the boat conformation. The chair conformation is the focus of this summary and is shown below. The carbons are tetrahedral so have no angle strain, and, as the Newman projection shows, the bonds are staggered so there is no torsional strain. The boat conformation suffers both torsional and steric strain. It will only be mentioned briefly and it is rare that undergraduates are asked to draw it.
The chair conformation of cyclohexane (& ball and spoke model for clarity).
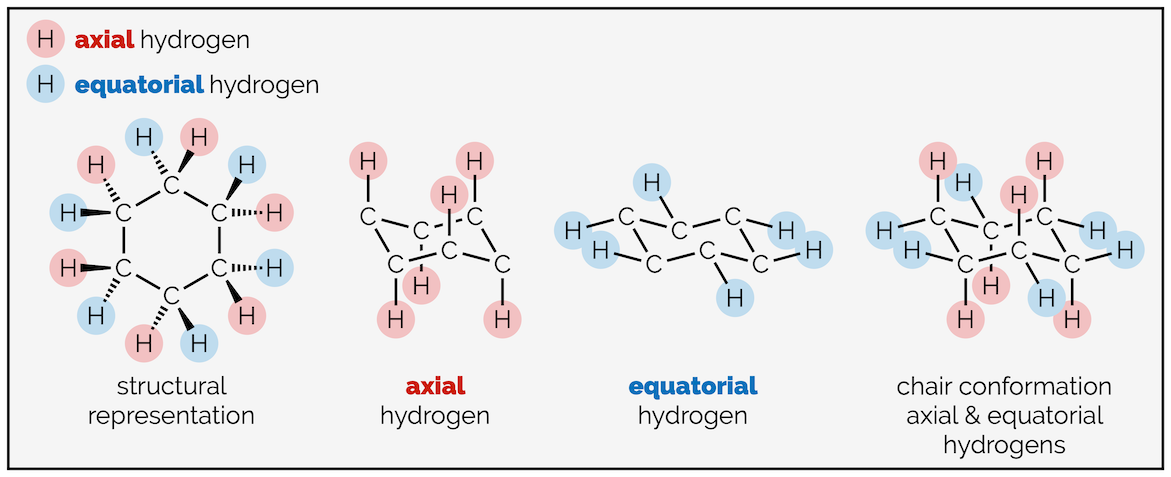
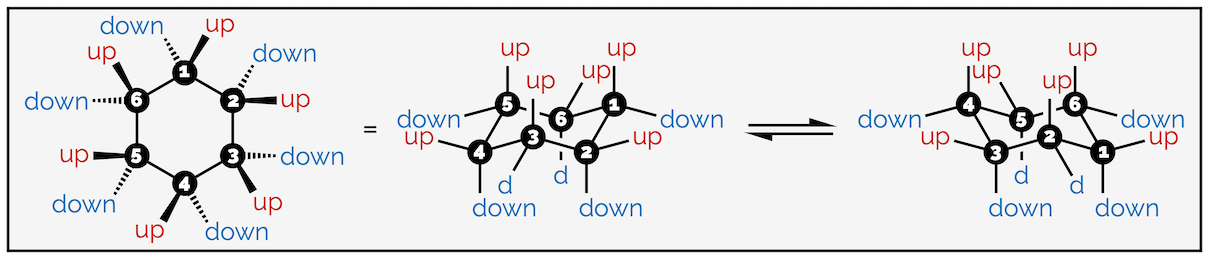
The hydrogen atoms of cyclohexane exist in two environments. There are six axial hydrogen atoms perpendicular to the ring. Three of these point vertically upwards and three point downwards. This means three are above the plane of the ring (up) and are represented as bold wedges on the standard 2D hexagon. There are three below the plane (down), which are represented with hashed lines. Note on the forced perspective chair that the upwards axial hydrogens alternate around the ring.
The skeletal representation of cyclohexane showing hydrogen pointing towards viewer (up) as bold wedges and downward hydrogen as hashed lines. The forced perspective representation of the ring shows three axial hydrogen are up and three down. Three equatorial hydrogen are up and three down.
The other six hydrogen atoms are equatorial. These stick out away from the ring when it is drawn as a chair. Again, three are upwards and three are downwards and they alternate around the ring.
Drawing the chair conformation of cyclohexane
Before discussing the conformations of cyclohexane and how different substituents or groups on the ring effect the conformations, it makes sense to learn how to draw the chair conformation. On the intertubes, you can find 100s of videos/explanations of how to draw the chair. Below is how I draw it (but, strangely, not how I normally teach it).
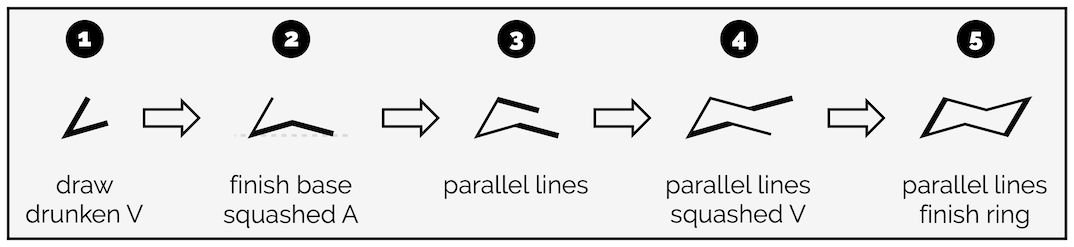
The key is to draw one bond at a time. Never try and draw all six bonds together (joined up handwriting). It will lead to a mess. Trust me.
Draw two bonds making a drunken V. The bond angle is around 45° but don’t get hung up on it.
Next draw a bond that finishes the base of the ring. It will end level to the point of the V. It looks like a squashed A.
From here you are simply drawing parallel lines. Add a bond parallel to the one you just drew.
Next draw a bond parallel to the base. This will make the top of the ring look like a squashed V.
Finally, complete the ring with a bond parallel to the initial drunken V.
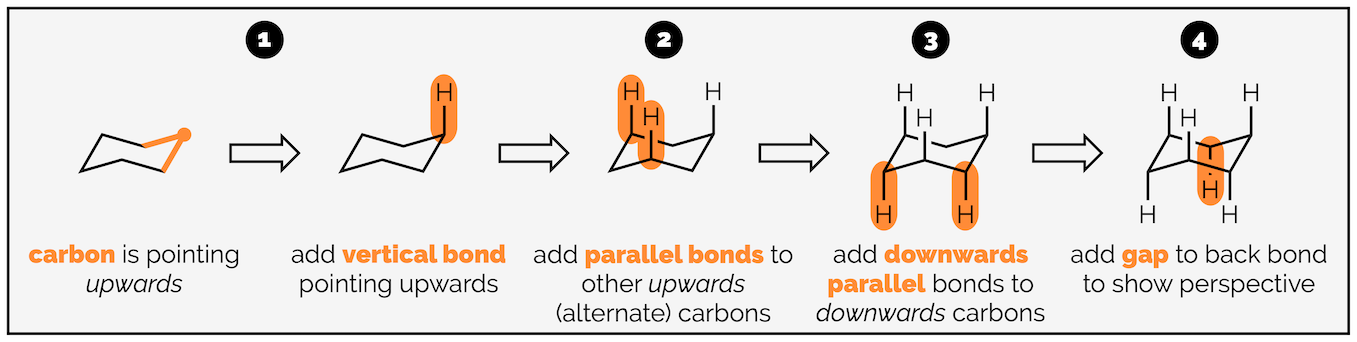
The next stage is adding the hydrogen atoms (or bonds to substituents). The key tip here is to remember that each carbon is tetrahedral, so you should try and draw it as a tetrahedron. I’m going to start with the axial hydrogen atoms. There are three axial bonds going vertically upwards and three axial bonds going vertically downwards. The upwards bonds come off the atoms or corners pointing upwards.
Start with the carbon atom in the top right corner and add a bond vertically upwards.
Now add two parallel lines on the two other atoms that point upwards. The three vertically upward bonds are on alternating atoms.
Repeat the procedure for the atoms at downwards corners. These bonds go vertically downwards.
Note the bond to the carbon at the back is broken so that it doesn’t cross the bonds of the ring. This gives the drawing a sense of perspective.
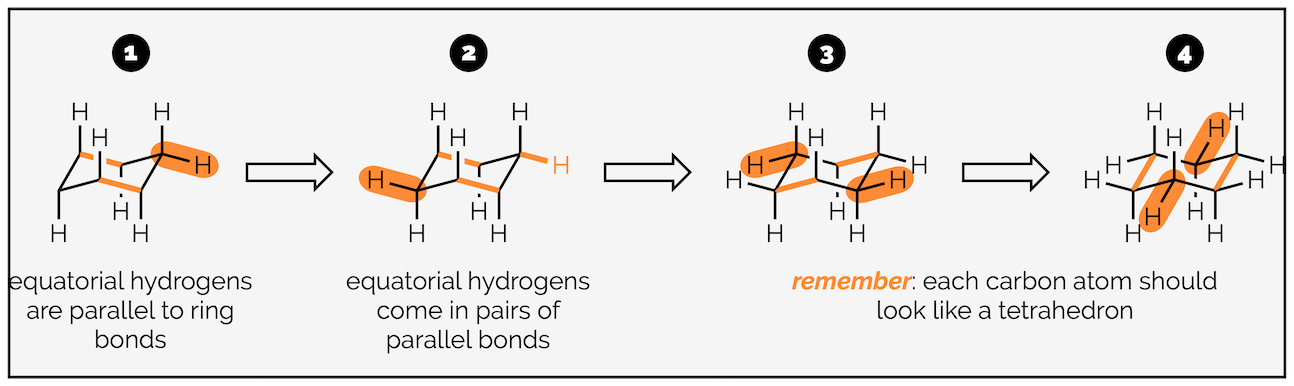
The next six hydrogen atoms are in the equatorial position. In theory these should be easier to draw (as long as you have drawn the chair ring correctly) as they are all parallel to bonds of the ring.
Starting with the top right hand carbon, draw a bond parallel to the central C–C bonds.
Repeat for the bottom left hand carbon. This bond will be parallel to the central C–C bonds and the bond you drew in step 1.
For the central carbon atoms, draw bonds that are parallel to the outside C–C bonds.
For the remaining carbon atoms, draw bonds parallel to the other two C–C bonds.
The chair can be drawn in the other direction as well. To do this start on the right-hand side of the molecule and draw the drunken V falling in the opposite direction. This chair is important when we consider ring flipping.
The chair can slope in the opposite direction, just start with the V falling to the left.
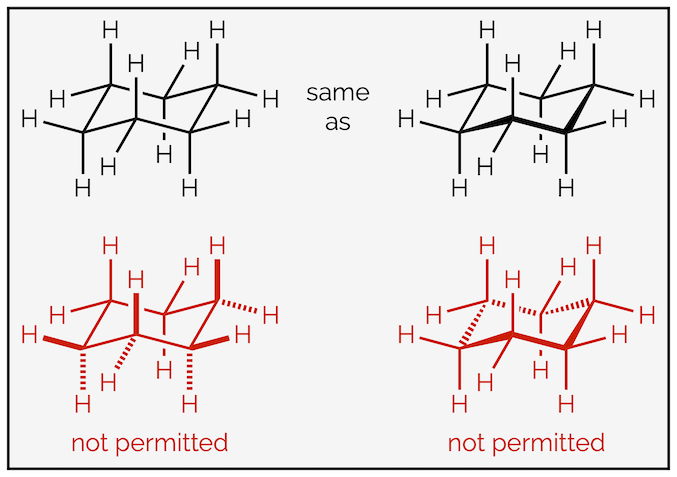
This representation of the chair conformation of cyclohexane forces perspective into the drawing. The shape can be further emphasized by highlighting the front bonds as coming out of the plane of screen. Chemists are very particular about how they draw the chair (thanks IUPAC), and by convention, you can only bold the three front ring bonds. You never bold (or hash) any of the bonds coming off the ring, the forced perspective informs you of their direction. You never use hashed lines in the ring itself. For those of you interested the rules of drawing are vast … HERE … and show that it is not your instructors that are being pedantic.
By convention, it is assumed that the chair conformation forces perspective onto a drawing. The use of bold wedges and hashed lines is not encouraged.
Take care when drawing the chair. Poor drawings lead to confusion and wrong answers. If you drawings look like below then start practicing:
Poor drawings all lecturers have seen far too many times.
An aside: Other uses of the chair drawing - might be found HERE.
Cyclohexane with a single substituent
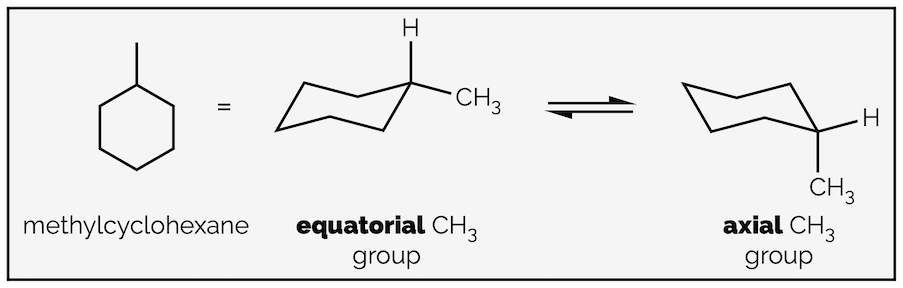
Replacing a hydrogen atom with another group leads to two possible structures, one with the new group in an axial position and one with the new group in an equatorial orientation.
The two conformations of methylcyclohexane.
The two structures are different conformations of the same molecule and are interconvertible through the rotation of C–C bonds. This process is known as ring flipping and it takes the molecule through a number of disfavored transition states or barriers to rotation. These are higher energy conformations. You don’t need to know how to draw them (at first year) but an approximation of ring flipping is shown in the gif below:
An animation showing ring flipping in cyclohexane.
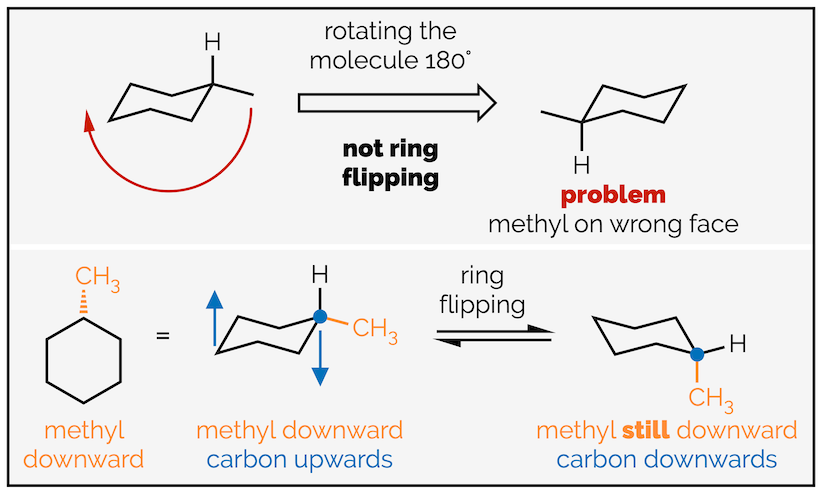
For most undergraduate courses it is unnecessary to know the names or energies of all the conformations cyclohexane passes through during ring flipping. What is important is that all the axial and all the equatorial groups swap. A common misconception is that ring flipping involves rotating the molecule (or is flipped … see where the confusion arises). It doesn’t, only the bonds are rotating. Each carbon that was pointing upwards rotates and points downwards. The groups on each atom are still on the same face of the molecule; if they started on the top face they are still on the top face but they will have swapped from equatorial to axial or vice versa.
Rotating the molecule versus rotating bonds or ring flipping cyclohexane.
There are two methods to draw the two conformations caused by ring flipping. The first (top row) shows the ring flipping by moving atoms up or down. It requires you to draw the two different chairs, one slanting to the right and one slanting to the left. It is probably the best representation of what is actually happening.
Two approaches to drawing the two conformations of cyclohexane: top is ‘more’ correct & the bottom is ‘easier’.
The second method is a bit of a trick but, as long as you understand why it works, it is easier/quicker. This involves drawing the same chair twice (same direction of slant). On the first draw out the molecule as normal, placing your group on an upward carbon atom. On the second move the group to an adjacent, downward atom. This will give you the second conformation. I find this easier, as my right-slanting chairs are much neater than my left-slanting ones, but it can lead to errors with the unwary.
Which conformation is favored?
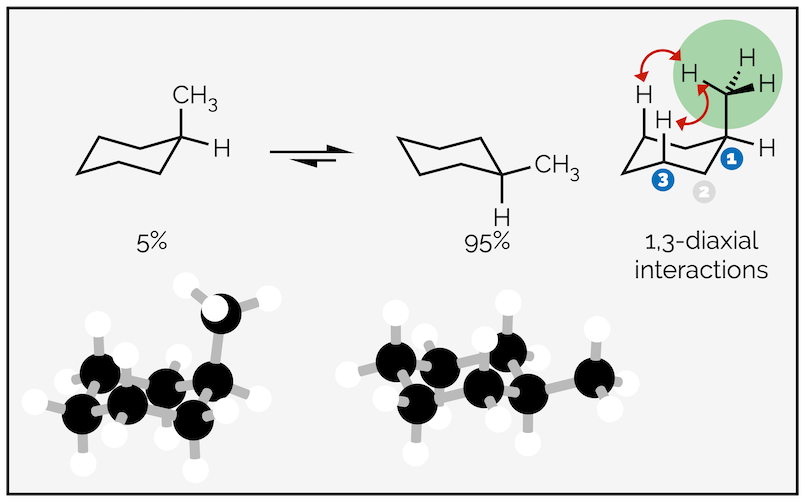
In simple systems, the substituent or group coming off the ring favors the equatorial position. Groups adopting the axial position are disfavored or higher in energy due to steric strain called 1,3-diaxial interactions. This is the steric interaction between multiple groups in axial positions as shown below:
1,3-Diaxial interactions disfavor the axial conformation and only 5% of the molecules reside in this conformation at any one time.
The larger the substituent and the larger the steric strain or the greater the 1,3-diaxial interactions. Replace the methyl group above with a tert-butyl group and the equilibrium favors the equatorial conformation almost exclusively with less than 1% of the molecules residing in the conformation with an axial tert-butyl group.
The larger tert-butyl group causes more steric or 1,3-diaxial interactions when in the axial position than a methyl group. It is rare to see a tert-butyl group adopt the axial conformation.
The disfavored interactions experienced by axial substituents can also be explained by looking at the Newman projection of the ring. In both chair conformations, the bonds are staggered so there is no torsional strain, but when the group is axial it is gauche or synclinal to the the ring and this results in steric interactions. If the group adopts the equatorial position it is antiperiplanar to the ring. This minimizes interactions.
Newman projection showing axial substituents suffer from gauche steric interaction.
Two, or more, substituents
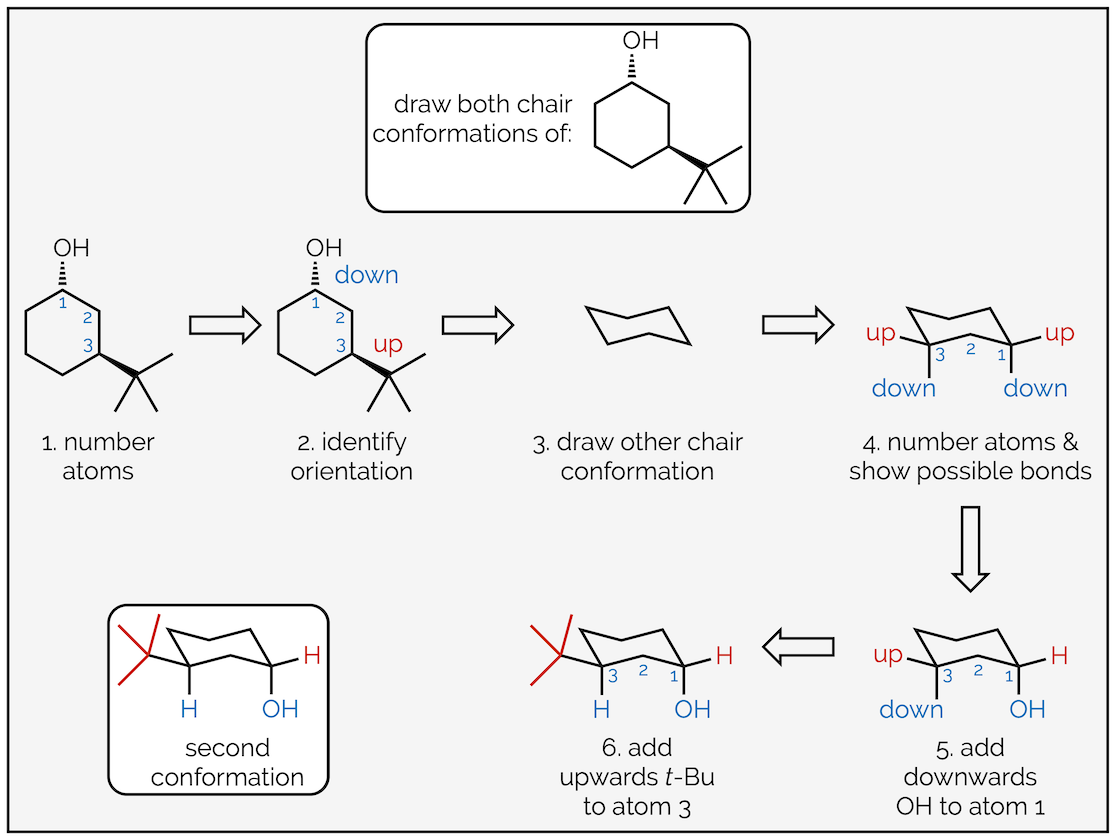
Ring flipping is possible when there are multiple substituents attached to cyclohexane. Of the two possible chair conformations, the one that has the largest group equatorial will be favored. The process for drawing the two conformations is identical to above, you map the groups from a skeletal representation onto the chair conformation.
Mapping substituents from the skeletal representation to the chair conformation.
To draw the two chair conformations of the molecule below follow these steps:
Drawing one of the chair conformations of a disubstituted cyclohexane ring.
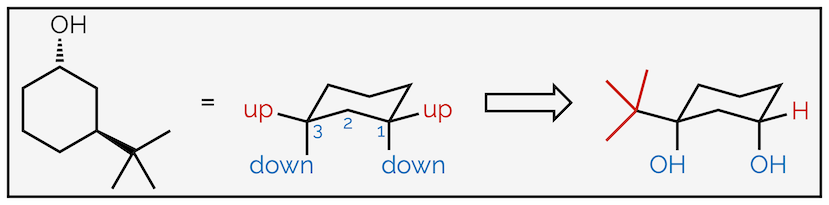
Follow the same process as before; first, number the atoms with substituents and indicate which face they are on. This is to ensure that you place them in the correct place on the chair. Next draw the chair conformation. Number the atoms and show where the axial and equatorial positions are. If you can’t work it out, draw them all then number the atoms. Next add one of the groups to the ring. In this case the hydroxyl group or alcohol is pointing downwards (a hashed line) and has been drawn in one of the downward equatorial positions. You could have drawn it in a downward axial position, it doesn’t matter (and we’ll draw that second conformation next). But, once you have put the first group on the cyclohexane ring it does matter where the next ones go. In this example, the tert-butyl group is upwards and on the third carbon so it must be axial.
Drawing the other chair conformation of a disubstituted cyclohexane ring.
To draw the second conformation, draw the chair conformation that slants in the opposite direction. Number the atoms again, but be careful. If atom #1 was an upwards carbon in the first drawing it must be a downwards carbon in the second. After that, all the steps are the same. This time the alcohol is axial (but still downwards) and the tert-butyl group is equatorial. Alternatively, you could have drawn the same chair, slanting in the same direction as the first conformation, but started numbering on the next carbon around. This would give the same result, showing the second conformation but just rotated through 60° compared to above.
A second way to draw the other conformation.
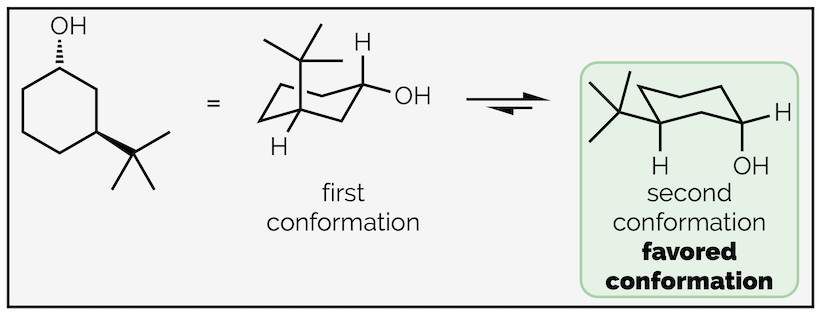
The two conformations are shown below. The most stable has the largest group equatorial as this minimizes 1,3-diaxial interactions.
The two conformations with the most stable, the one with the largest group equatorial, highlighted.
A common misconception (at least when I'm marking exams) is that all the substituents will be equatorial in the favored conformation. This is not always possible unless you break a bond. The relative stereochemistry of substituents on a ring must always be the same, regardless of the conformation. This means the substituents are always on the same face or opposite faces. If you draw two conformations and the relative stereochemistry changes between them, you have made a mistake and have drawn a diastereomer.
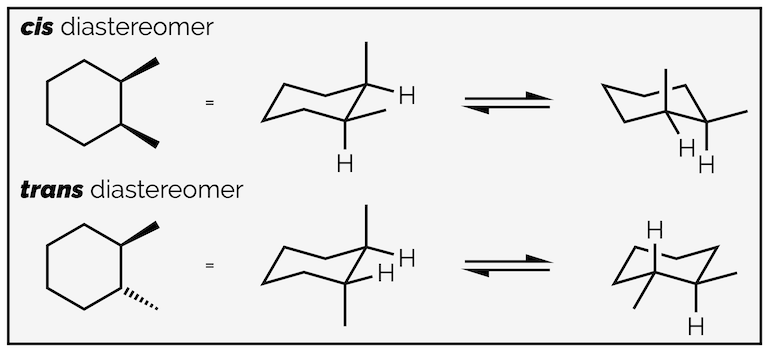
With disubstituted cyclohexanes the terms cis and trans are used to describe the relative stereochemistry. If the two substituents are on the same face of the ring (both up or both down), they are cis. If they are on opposite faces (one up and one down), they are trans. This is analogous to the naming of alkenes (if you aren't using the more useful E/Z nomenclature). Always check that both conformations have same relative stereochemistry.
Cis and trans diastereomers and their two conformations.
Other rings
The same principles hold for six-membered rings containing hetereoatoms as long as those atoms are sp3 hybridized. For instance, the tetrahydropyran below can be draw in two different chair conformations.
Six-membered saturated heterocycles behave similar to cyclohexane.
Nitrogen heterocycles, such as piperidines, behave in a similar fashion. The trick here is that it is unnecessary to define the stereochemistry of the group on the nitrogen atom. It is able to change face and will always be equatorial (in simple examples). This is due to a process known as pyramidal version. That’s a story for another day.
Conclusion
This was a longer introduction to the conformations of cyclohexane than I would have liked. It has highlighted that cyclohexane can adopt a conformation that minimizes torsional and ring strain. This is the chair conformation. Substituents on the chair can exist in two different environments, either be axial or equatorial. The chair conformation of cyclohexane can rotate through a process called ring-flipping into a second chair in which all the axial substituents have become equatorial and all equatorial groups are now axial. Of the two conformations, the molecule will favor the one that places large groups in the equatorial position as this minimizes 1,3-diaxial and gauche interactions.
A ring of six sp3 hybridized is an important motif, and any carbon atoms can be swapped out for other sp3 hybridized atoms. The resulting ring will adopt the same chair conformation. This is important in the chemistry of carbohydrates/sugars and other biologically relevant molecules. The arrangement of six atoms is also important for predicting the stereochemical outcome of many reactions. It is a valuable skill to be able to draw and manipulate the chair conformation and I would recommend practicing.
As with all of these summaries, this is just the introduction to this chemistry. The stability of the conformations has been argued on steric grounds only. Electronics can have an important affect as shown by the anomeric effect and the conformation of some dihalides, but that is chemistry for a later summary.
As always there should be some practice questions HERE.