Simplified Rates of Reaction from an Organic Chemist
Introduction
Rates of reactions, and reaction kinetics, is a topic often skipped over by organic chemists. It is mentioned in the discussion of the classic substitution reactions (SN1 & SN2), and as a vague concept in catalysis (catalysts speed up reactions), but it otherwise left to physical chemists to teach. This is a mistake (interpret that statement however you want!). An understanding of the rate of a reaction, and the kinetics of a reaction (without going into mathematical detail) is very useful for a synthetic chemist. How fast a reaction occurs is important in biology, environmental science, and many other disciplines. Here is a muddled overview (I have never taught this subject so I'm a little rusty and don't have any of the normal 'lecturer's tricks/insights' that I hopefully do for other topics).
There are lots of reasons the rates of reactions and kinetics is important. How long pharmaceuticals stay in the body before being either broken down or excreted is an obvious example. Similarly, the lifetime of herbicides and pesticides in the environment is of vital importance. The rate these are broken down can have devastating consequences. Many of the reactions that we require to keep our bodies functioning are too slow to be of use without enzymes accelerating them. To truly appreciate synthesis you need to understand the mechanism and this can only be determined through kinetics. The list of why we should have a vague appreciation of kinetics is huge. Hopefully, I will not make too many mistakes and so this will be a useful introduction. Actually, I hope someone else has taught you properly and this is just a reminder ...
Chemical Reactions
Whether a reaction is favorable, meaning the products are more stable than the starting materials and that ΔG is negative, is only half the story. The speed at which the reaction occurs is equally important. Consider the combustion of isooctane, a hydrocarbon found in petrol, an essential process in combustion engines. Thermodynamically, this is a very favorable reaction with ΔG = –1000 kJ mol–1 at 298 K (room temperature).
The combustion of isooctane is thermodynamically favorable, with the equilibrium far are on the right-hand side. But the reaction does not spontaneously occur at any appreciable rate. It is said to be kinetically stable. We must put energy into the reaction to promote it.
If you have read the summary on equilibrium HERE, you will possibly remember that such a large, negative value of ΔG leads to an equilibrium constant of K = 5.13 x 10176 (as K = e–ΔG/RT). This a mind numbingly large number. There is nothing I can compare this number to, it is just so big. There are fewer (or is it 'less' as you cannot really count the number of atoms) atoms in the universe. The reaction is irreversible. And yet, we can pour petrol into the tank of a car, in the presence of oxygen (air is 21% oxygen) and nothing happens. It turns out that the reaction requires the input of energy to initiate it. It needs a spark. Only then it will proceed to equilibrium (pretty spectacularly if you are not careful). A negative ΔG is necessary for a spontaneous reaction but it is not sufficient for the reaction to actually occur. There is another factor to consider and that is the kinetics of the reaction.
We can start to look at this pictorially. The two energy diagrams below show thermodynamically favorable and disfavorable reactions.
A reaction is thermodynamically favorable if the products have less energy than the starting materials. This is shown on the left. A product is thermodynamically less favorable (or disfavored) if the products have more energy.
Such diagrams tell you which compounds are more thermodynamically stable and will be favored in an equilibrium. But, they don't tell you how fast the reaction is. The reaction could reach equilibrium in the blink of an eye or take thousands of years. If you add the familiar curved line connecting the reactants to the products, a line that shows how the energy of the system changes over time or the progress of the reaction, then there are now clues as to the rate of the reaction.
On an energy profile, the line connecting reactants and products is related to the energy changes in the system as a reaction progresses. The higher the energy barrier, the saddle point between the reactants and products, the slower the reaction will be.
The reaction profile shows how the energy of the reacting system changes as the reaction progresses. A common feature of all reaction profiles is that the energy rises first, regardless as to whether the final products are more or less stable than the reactants. This means that you must put energy into a reaction before it will start.
Consider a block of wood standing on its narrow end. You want to push it over so that it ends up lying flat on the floor. The process is favorable, the block is more stable lying horizontal rather than vertical but it still takes energy to tip it onto its edge. A weak push has insufficient energy, the block wobbles but returns to its original position. A strong push, using sufficient energy, moves the block beyond a certain point, and now it is impossible to stop it falling. You have given it sufficient energy that will now reach its most stable state.
An analogy for activation energy. A block balanced vertically is not in its most stable state but it will stay balanced. If you give it a weak push, it will wobble, but it will not fall over. There is a minimum amount of energy you must supply before it falls over and reaches its most stable state. This is its activation energy. Molecules behave in the same manner.
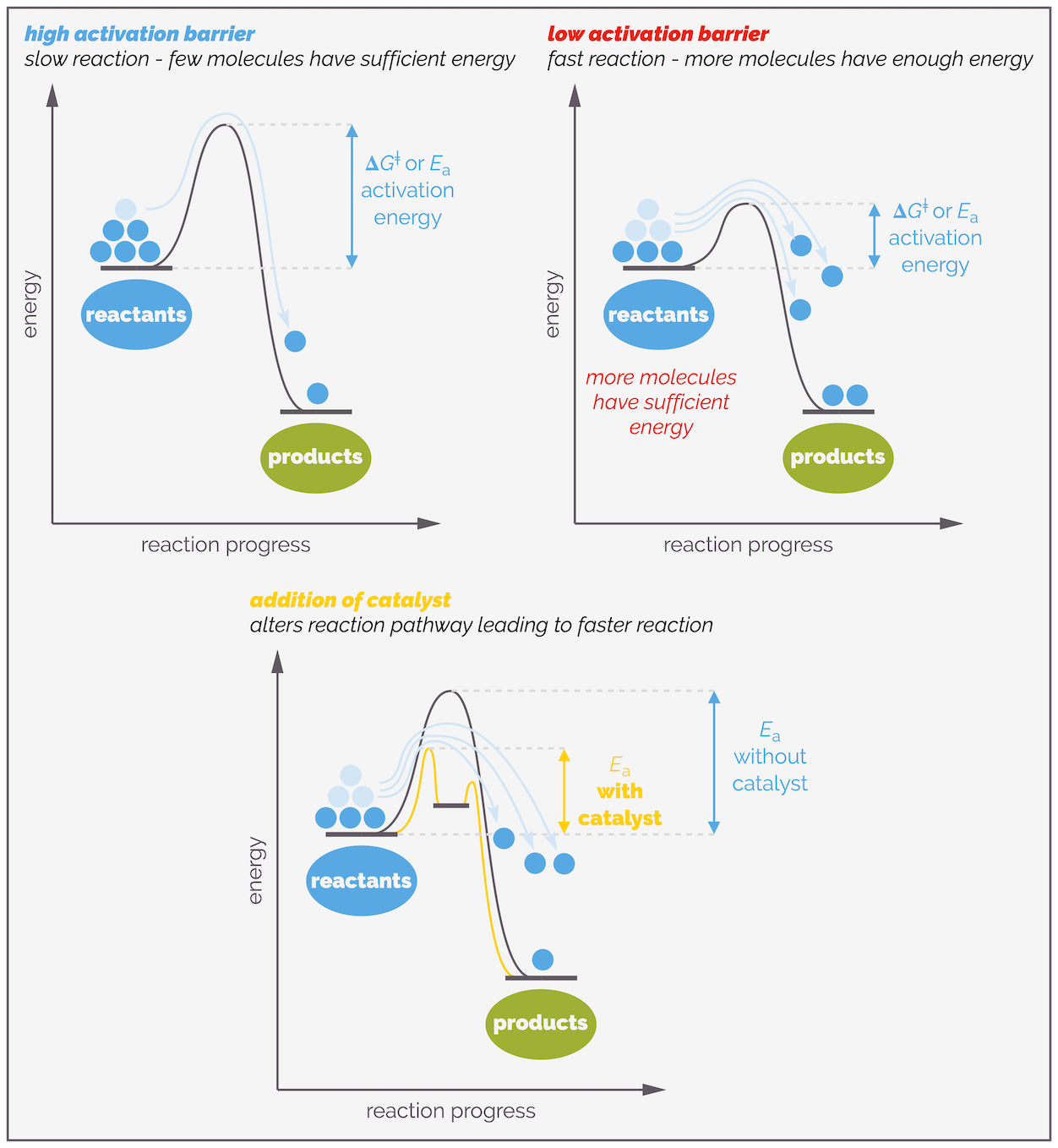
Reactions behave in the same manner. You need to introduce energy before to start the reaction. This energy barrier to reaction goes by many names, it is called the activation energy or the activation barrier. It is given the symbol Ea or ΔG‡. A reaction can be thermodynamically unstable, meaning the products are far more stable than the reactants but the mixture might be kinetically stable as the energy barrier to reaction is too big and the mixture will not react unless it is given a push.
The larger the activation energy the slower the reaction. The smaller the activation energy, the easier and faster the reaction will be. The reaction profile tells you about two properties of the reaction. The difference in energy between the reactants and the products is the thermodynamics of the reaction. This tells you which molecules are more stable and the position of the equilibrium, which side of the reaction is favored. This is the bottom half of the diagram. The top half of the diagram shows the activation energy. This tells you about the kinetics of the reaction, or how fast the reaction can occur. The key point is the peak of the curve, this is the transition state, or the ideal arrangement of atoms, in an ideal conformation with charge separated over partial bonds, that is required for the reaction to proceed. I’ll be talking more about this later.
A reaction profile showing both where we learn about thermodynamics, with the energy of the reactants and products determining the position of the equilibrium, and kinetics, the activation barrier that controls the rate of reaction. Organic chemists can be quite vague/lazy/imprecise about energy (hence the lack of a plimsole °) sometimes using E as energy, G as Gibbs free energy and H as enthalpy. These don’t actually mean the same thing and it must be really annoying for physical chemists.
A number of factors control the height of the energy barrier or activation energy. Even more factors influence which and how many molecules can overcome this barrier. Together, this controls the rate of reaction and will be the subject of the rest of this summary.
The Rate of Reaction
The rate of a reaction is a measure of the change in concentration for the disappearance of reactants over a unit of time or the change in concentration for the appearance of product over a unit of time. This is analogous to the speed of a car. Speed is a measure of the distance traveled in a unit of time, while the rate of a reaction is a measure of the change in concentration in a unit of time:
Speed is a measure of movement or a change in distance per unit of time (commonly in either km per hour or miles per hour). The rate of a reaction is a similar measurement. It is the change in concentration of a reactant or product per unit time. In this example, the measurement is of the disappearance of reactant (blue circle). As a result, we have had to add a minus sign to the equation. This ensures that the rate is positive (negative rate doesn’t make sense … it is like saying a car is traveling at -30 kph, it is meaningless).
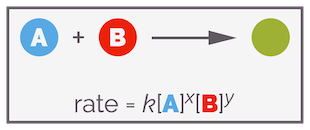
Now we know that the rate of a reaction concerns a change in concentration of reactant or product per unit of time but this doesn't tell you anything about what controls the rate of a reaction. Let's consider a simple reaction involving a nucleophile attacking an electrophile, you can generalize this as the nucleophile A + electrophile B gives product C.
A simplified general reaction involving two reactants.
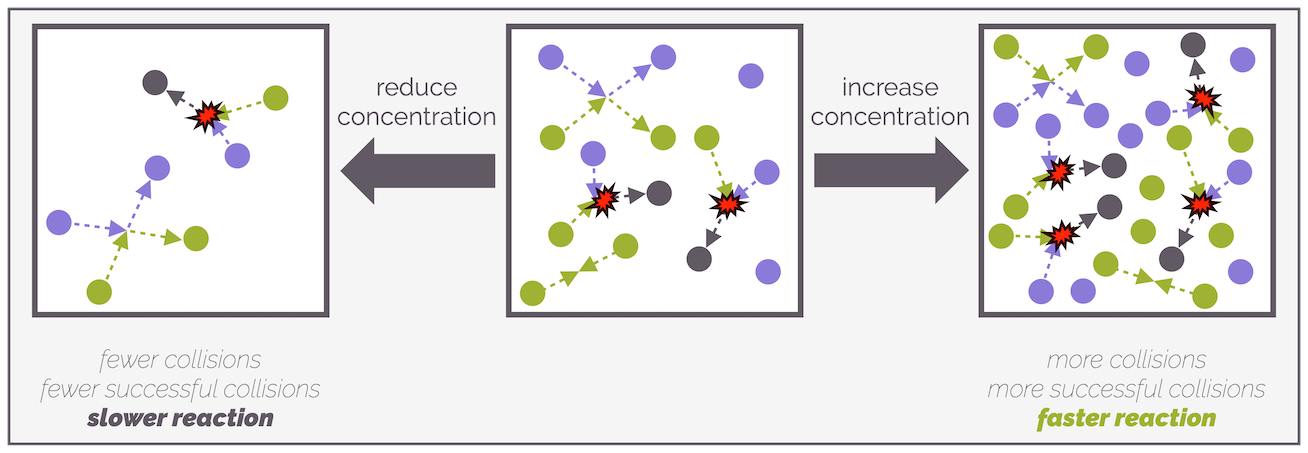
One model that explains the rate of a reaction is collision theory. This states that a reaction can occur when two molecules collide in such a manner as to cause a change in the bonds. The more of molecule A there is, the higher the concentration and the fast the reaction as there is a higher frequency of collisions. Similarly, the higher the concentration of B, the greater the frequency of collisions (the greater the number of collisions per unit time) there can be and the faster the reaction is. Conversely, reduce the concentration of either reactant and the frequency of collisions decreases (there are less collisions per unit time). This means the rate decreases. The rate of reaction is proportional to the concentration.
The rate of reaction is proportional to the concentration of reactants A and B.
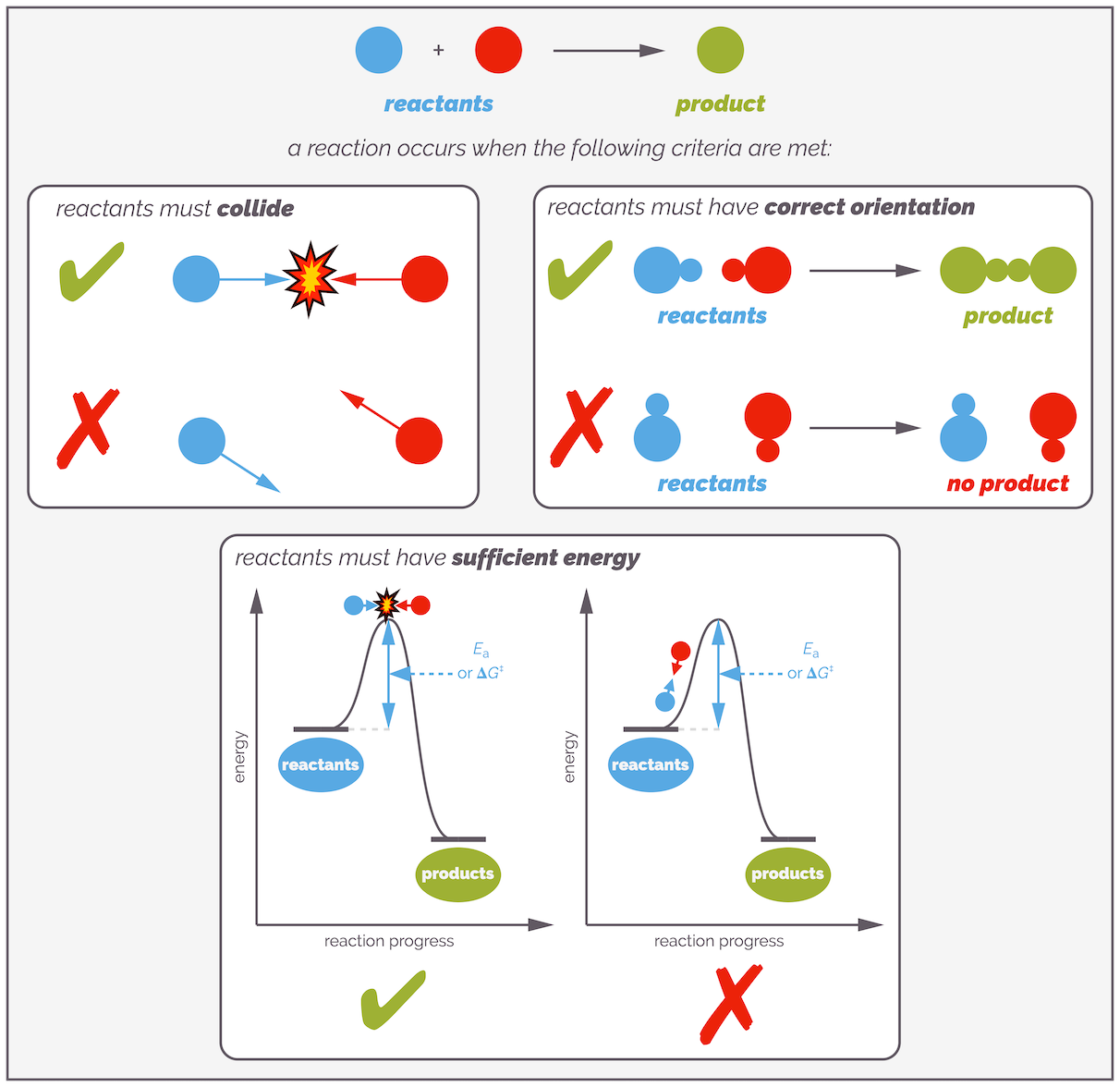
Of course, it is not as simple as that. Not all collisions lead to a reaction. Sometimes two molecules will hit each other and just bounce off. They will change the heat of the reactants, causing the bonds to stretch or vibrate but not break and react. For a collision to be successful, the reactants must have sufficient energy to cause a reaction. They must have more energy than the activation barrier. Additionally, the molecules must meet with the correct orientation. You can think of the collisions being like a game of pool and a reaction only occurring when a ball is sunk in a pocket. To pot a ball and achieve a reaction, the cue ball must collide the target at the correct angle and with sufficient force or energy to allow it to reach the pocket. Failure to meet either of these criteria and you will not sink the ball in the pocket (there is no reaction). This is just an analogy, it is the orientation of the molecules not the direction they collide that is important (as you will hopefully see).
Collision theory treats reactions a little like snooker or pool. For a reaction to occur, two balls (molecules) must collide at the correct orientation and with sufficient energy. If either of theses conditions is not met, the molecules collide but do not react. Obviously, there are differences between collision theory and pool. The main one being that more than one 'shot' is occurring at any moment.
Normally, students readily understand why molecules need sufficient energy to react (breaking bonds takes energy and you only get compensated (energy back) when a new bond forms), but the orientation requirement is a little more confusing (especially if you haven't seen any molecular orbitals). A common example to demonstrate the importance of orientation is to consider the protonation of an alkene as observed in a reaction such as hydrobromination (see HERE). The carbocationic intermediate is formed when the alkene is protonated. This requires the alkene and acid to collide, but the collision is only successful if the hydrogen atom approaches the π bond. There are many unsuccessful collisions when the acid approaches the wrong part of the alkene (substrate) or approaches bromine atom first. In all these cases, the two molecules just bounce off each other. (Of course, I've ignored the fact that if the reaction is performed in a solvent with a lone pair of electrons then the hydrobromic acid is fully dissociated and protonation involves a species such as a hydronium ion, but I think you get the general idea).
Not all collisions are successful. Molecules must collide with the correct orientation for a reaction to occur. This can be pictured if you consider protonation of an alkene. For reaction to occur, the hydrogen must interaction with the π bond of the alkene. Any other clash will lead to the two molecules simply bouncing off each other.
The idea that not all collisions are successful allows you to add a correction factor to the simple rate equation above, and now it looks like this (but please note, this is not the finished equation, we need one more concept before we’re finished and that will be introduced later).
A simple version of the rate equation (not complete yet ... see later), where k is the rate constant and [A] & [B] are the concentrations of the reactants A & B.
The correction factor, k, is called the rate constant and it is unique to every reaction at a specific temperature. It is an experimental value meaning that unlike a value such as the equilibrium constant, it must be derived from measurements and cannot be calculated from first principles (or at least, that is my understanding, but I confess physical chemists are cleverer than me and so they might be able to calculate it). Effectively, the rate constant hides (contains?) information about the activation barrier, the frequency of collisions and the chance of one of those collisions being successful.
Changing the Rate of Reaction (Collision theory)
Concentration
Inspecting the rate equation shows that an increase in the concentration of either reagent will increase the rate of reaction.
If you increase the concentration of one of the reactants, the rate equation shows that rate must also increase. As you shall see later, this isn't always true and isn't always straight forward but it gives a good point to jump off in our discussion.
The more molecules present, the greater the frequency of collisions that will occur and this leads to more reactions. Increasing the concentration, especially of just one reactant, promotes unsuccessful collisions between two identical molecules (A+A or B+B) as well as the successful collisions.
Reducing the concentration of reactants reduces the frequency of collisions, successful or otherwise. A lower frequency of collisions (fewer collisions per unit time) leads to a slower reaction or a reduced rate of reaction. Increasing the concentration of reactants increases the frequency of molecules colliding and there will be more successful and unsuccessful reactions, the reaction will be faster or the rate of reaction increases.
Temperature
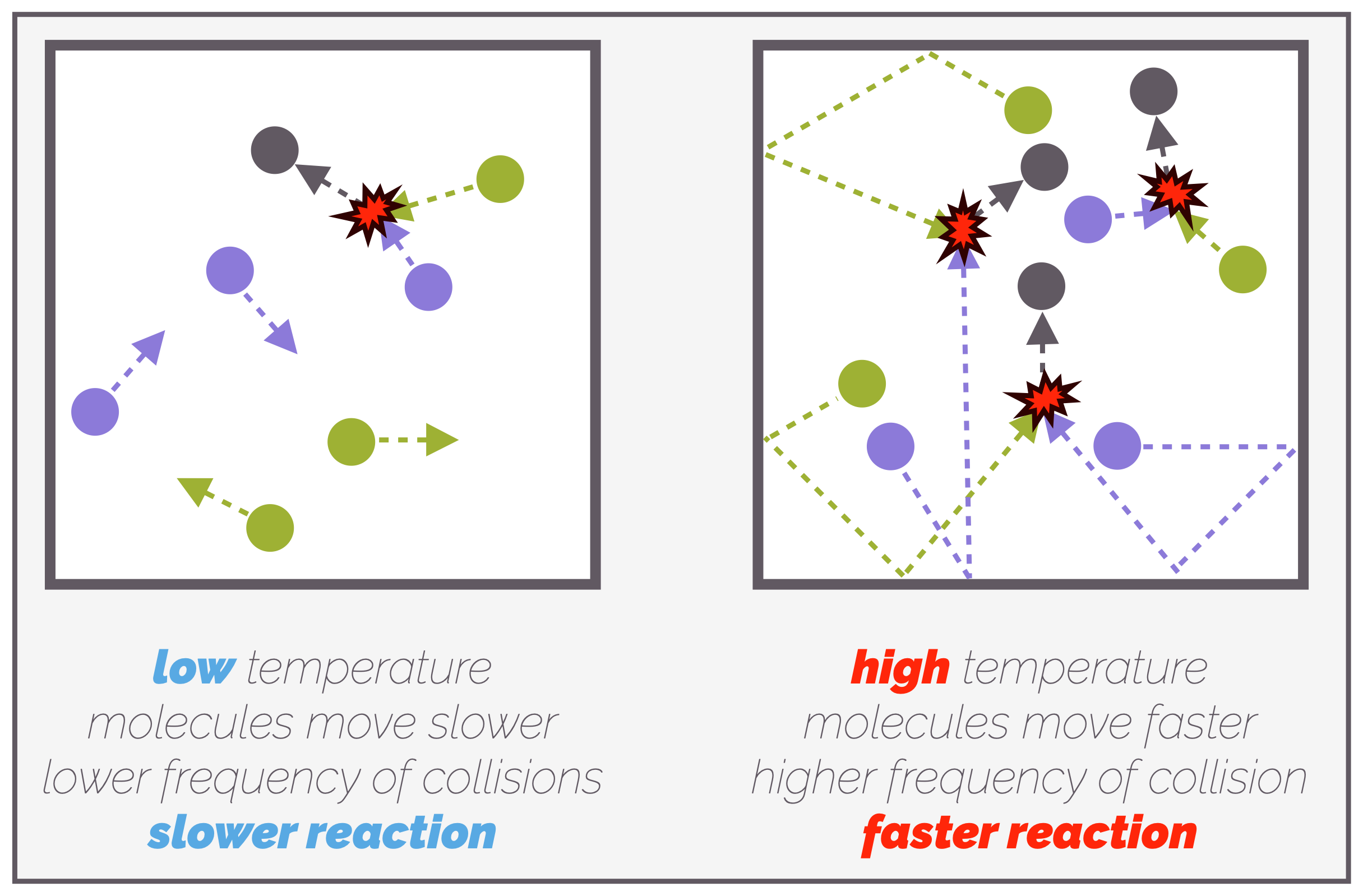
Raising the temperature of a reaction leads to a higher rate of reaction for two reasons. As molecules are heated they start to move faster and this increases the frequency of collisions, which, in turn, leads to more successful collisions and the reaction speeds up.
At low temperatures, molecules are moving slowly and there are only a few collisions per unit time. Not all of these are successful, the reaction is slow. At higher temperatures, the molecules have more energy and are moving faster. The frequency of collisions increases and this leads to an increased frequency of successful collisions. The rate of reaction increases.
The second reason heating a reaction increases the rate is that more molecules now have sufficient energy for a successful collision. Remember, for a reaction to occur, not only do the molecules need to meet (collide) but they must have enough energy to overcome the activation barrier. Heating a reaction gives molecules more energy.
As the temperature of a reaction is raised so the number of molecules with sufficient energy to overcome the activation barrier increases. The more molecules that have sufficient energy, the higher the frequency of successful collisions and the rate of reaction increases.
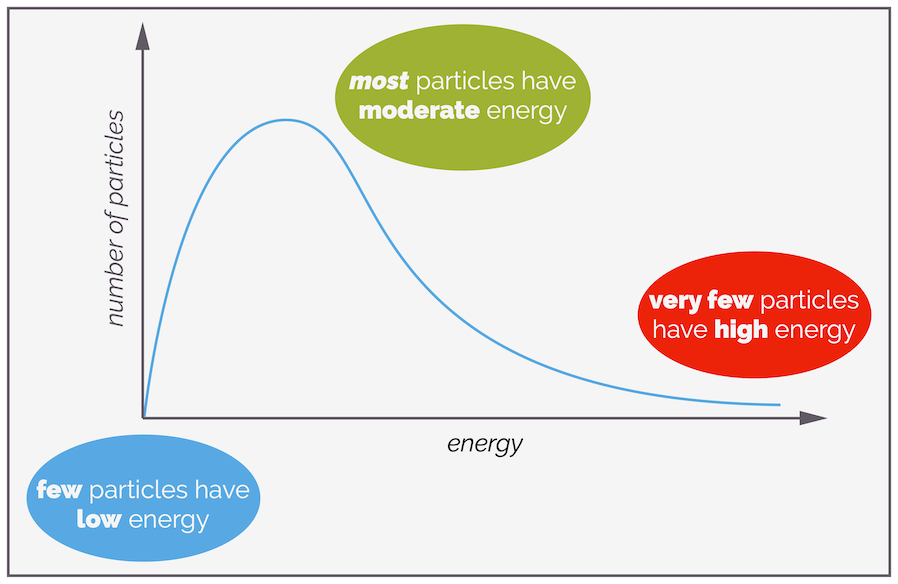
The effect of temperature on the rate equation is harder to see as it is hidden in the rate constant, k. Molecules don't all have the same energy, some are moving quickly, some more slowly. Some will collide and gain energy while others lose energy. The amount gained or lost depends on orientation, where the molecules collide, what bonds can vibrate and many other factors. It is possible (for a gas) to plot the distribution of the number of particles that have various energies. This is the Maxwell-Boltzmann Distribution. While it is only for gases, you can use it as a model for liquids or solutions.
Not all molecules will have the same energy, and there is a distribution of energies that favors moderate or average (surprise) energy while there are fewer molecules with very high or very low energy. The shape of the curve is derived from maths/equations that you can get from a physical chemist (if you need it). Area under the curve is related to the number of molecules with that energy.
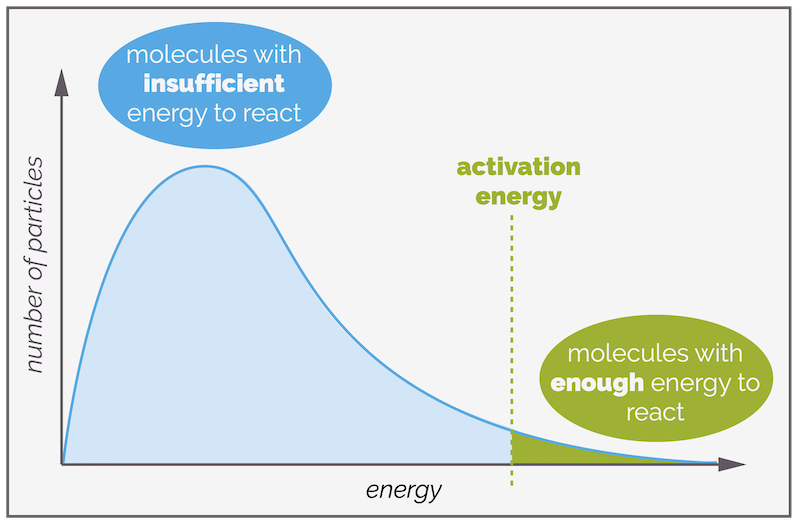
You can mark the activation energy or barrier onto this plot. The area to the left of the activation barrier represents the number of molecules that have insufficient energy. Collisions involving these molecules will be unsuccessful. The area to the right of the barrier is the proportion of molecules that will react upon collision as they have sufficient energy to overcome the reaction barrier.
The area under the curve to the left of the activation energy represents the molecules with insufficient energy to react. It is the majority of the molecules. To the right are those that have sufficient to cause a reaction. It is normally a smaller portion.
Increasing the temperature of a reaction increases the average energy of the molecules. The overall area under the line doesn't change, you haven't changed the number of molecules but it has shifted to the right, with the average energy increasing. The area to the right of the activation barrier is still small but it has increased significantly. This represents how many more molecules now have sufficient energy to react.
Increasing the temperature, increases the proportion of molecules that have enough energy to overcome the activation barrier and react.
There is a mathematical link between the rate of reaction, the temperature of the reaction and the activation barrier and this is known as the Arrhenius equation:
The Arrhenius equation.
The negative value of the exponential term (the bit in blue) tells you that the larger the activation energy the slower the reaction (the smaller k), and the higher the temperature the faster the rate. Basically, the blue term in the equation relates to the distribution of molecules that have the same, or more, energy than the activation barrier. The pre-exponential factor (A) is related to the number of collisions, and the probability that those collisions are successful.
The bottom-line of this long winded discussion is that if you increase the temperature, you will increase the rate of reaction, BUT ... and this is chemistry so there is always a but, raising the temperature doesn't necessary lead to more product. Raising the temperature increases all reactions, including non-desired processes that lead to unwanted side-products. Something, most of us practicing chemists have learnt at one time or another.
The Activation Energy/Barrier
The Arrenhius equation above shows that the rate of reaction is related to the activation energy or activation barrier. Lower the activation barrier and more molecules will have sufficient energy to participate in successful collisions and undergo reaction. This means that the lower the activation barrier, the faster the reaction.
A lower activation barrier means a faster reaction as more molecules will have enough energy to react. It is possible to lower the activation barrier by adding a catalyst. Such species change the reaction pathway and can add additional steps but all these steps will have a lower activation barrier than the original pathway.
Transition State Theory
Collision theory is a useful model that allows you to visualize many of the elements that influence the rate of reaction but it makes a number of assumptions or over simplifications. Transition state theory offers a more accurate alternative. It focuses on the activation energy and the structure of the transition state, the saddle point of a reaction profile. Where collision theory considered the molecules to be hard spheres, like pool balls, transition state theory takes into account the structure of the molecules. I don't think there is a need to go into detail here (I'm not a physical chemist and would undoubtedly butcher the explanation).
It turns out that physical chemists not only like to correct simple synthetic chemists like myself, but they love to discuss (read argue) amongst themselves as well. As a result, I’m walking into dodgy territory with this part of the discussion. It appears that there are multiple definitions, multiple opinions, and multiple arguments for many of the topics below. Something as ‘simple’ as the phrase ‘rate determining step’ is, in fact, far from simple, and possibly even meaningless. The sections below are written for undergraduates with a preference for organic chemistry. The definitions and arguments I have used are hopefully the ones you will find in undergraduate textbooks. Hopefully this is useful. If you are a physical chemist (or prefer physical chemistry) … why are you reading this? Sorry, more seriously, if you want a more in-depth discussion then you could do a lot worse than start with something like THIS. The dude who wrote this has an approachable yet accurate style (and has politely corrected some of my 1 page summaries … all remaining errors are definitely still my fault!).
When reactants are transformed into products the reaction could occur directly or it could proceed through one (or more), short-lived species. Two possibilities are shown in cartoon form below.
A reaction mechanism describes the sequence of elementary steps (or elementary reactions) that lead from the reactants to the product. An elementary reaction is a single step that cannot be broken down into a series of reactions. It is a direct transformation of reactants to products without an intermediate. A reaction mechanism is a composite of elementary steps with one, or more, intermediates formed along the sequence. Transition states frame each intermediate. And boy, do I dislike the curve of the far right!
The direct transformation of reactants into products occurs by a single elementary step. This is a reaction that cannot be broken down any further. The rate of such a reaction will be related to the stoichiometry of that step.
A sequence of elementary steps linked together to bring about the overall reaction is known as the reaction mechanism. In such an example, the rate of the reaction does not have to be related to the stoichiometry of the overall reaction. In fact, it rarely is. Just consider the combustion of isooctane at the start of this summary. The rate is not determined by 27 molecules meeting all at once. If it was, the reaction would never occur as the probability of that occurring is miniscule.
Transition state theory is only concerned with elementary steps. According to transition state theory, there is a point between where the molecules of the reactants have combined but have not become the product. This is known as the active complex or transition state. It has a definite geometry (arrangement of atoms) and charge distribution (bonds and partial bonds) but doesn't exist in any meaningful way. Transition states essentially have zero lifetime with the reaction passing through them but the reaction can never stop at this point. It is the point of maximum energy between the reactants and products. The energy of the active complex or transition state is the activation energy.
Transition state theory views each elementary step in the same way. There is a state where the molecules are neither starting materials or products. This is known as the active complex or transition state (there is a subtle difference, I think, between these two with the transition state being the apex of the curve while an active complex is the top portion of the curve (so there is a little more flexibility)). It is the saddle point of an elementary step meaning it has the maximum energy and is a transient species with no appreciable lifetime. Formation of the active species is reversible and it can break apart to give either the starting materials or the product. The rate of the reaction depends on the concentration of the active species, how easily it breaks apart and in which direction it breaks apart.
In transition state theory, the rate of reaction is related to the concentration of the active complex, the rate at which the active complex breaks apart, and the direction it breaks apart. Formation of the active complex is considered to be reversible or an equilibrium. It can break down to return reactants or break apart to give the product. All this means that unlike collision theory, which was largely empirical, with transition state theory it is possible to calculate the energy barrier and hence rate (I think).
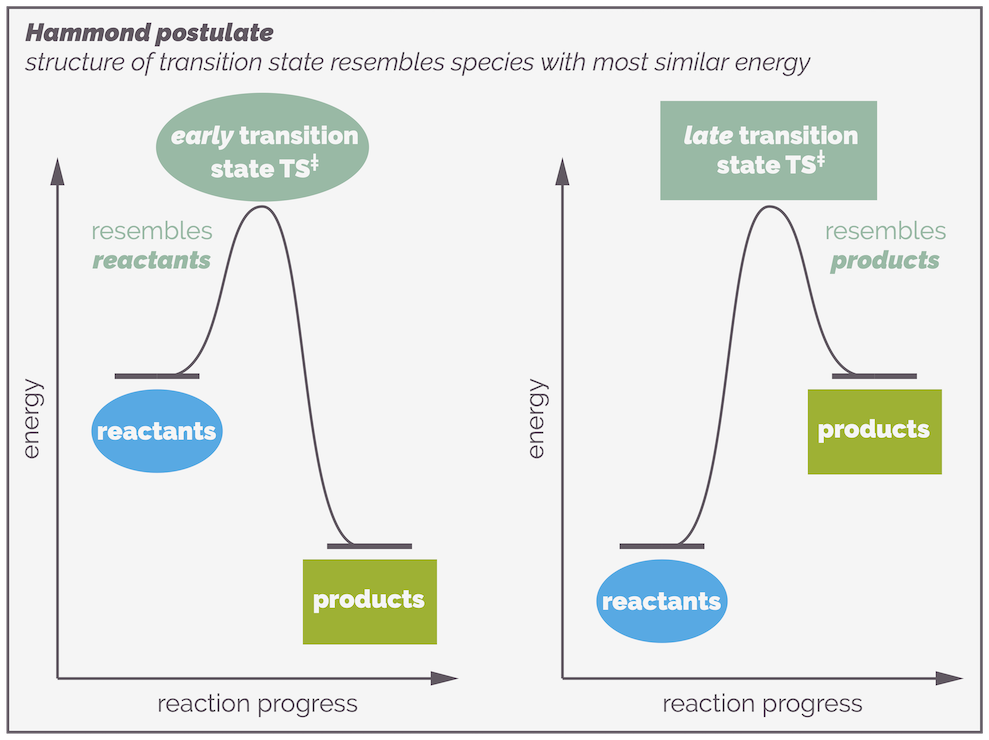
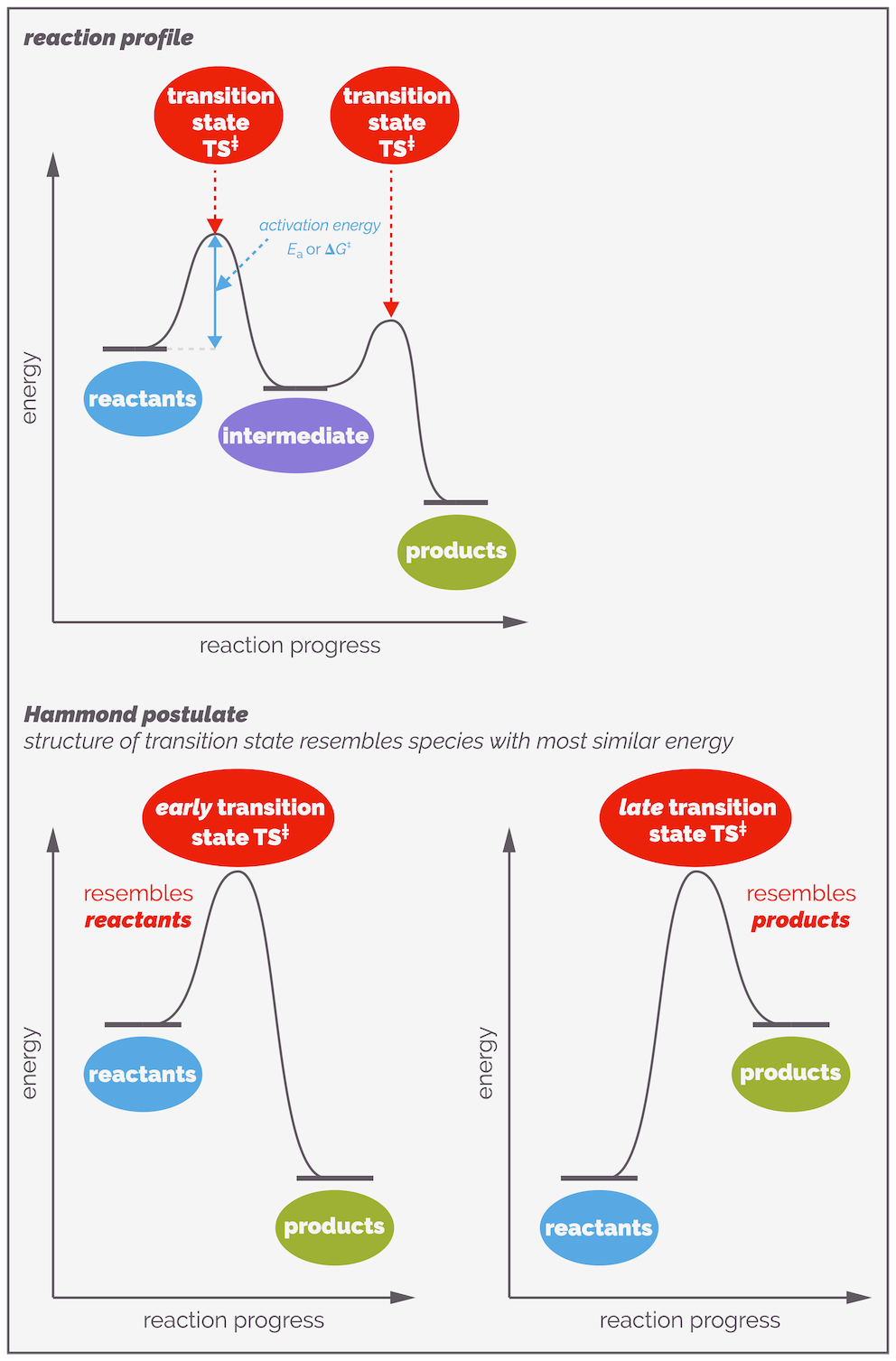
Because the transition state haws no lifespan, it cannot be isolated or even observed. But the structure of the transition state is really important. Fortunately, you can predict or guesstimate what it looks like. The Hammond postulate gives you a clue as to what a transition state might look like. It states that the structure of a transition state resembles the structure of the energetically nearest stable species (reactant, intermediate or product).
The Hammond Postulate states that the structure of the transition state resembles the structure of either the preceding or subsequent stable species along the reaction profile that it is is closest in energy to. In other words, in the examples above the transition state resembles the structure of the reactants if they are closer in energy to the transition state than the products (the left-hand side). Alternatively, if the transition state is closer in energy to the products, its structure will resemble that of the products.
For reactions with multiple steps, there will be multiple transition states. Sitting between a pair of transition states, there is a local energy minima or energy-well (a place of tranquility on the rough ride that is a reaction) known as an intermediate. Intermediates are real, they exist although their lifetimes are often short.
Stepwise reactions involve the formation of intermediates. These are local energy minima and represent real species that, while reactive, exist and in rare examples, can be isolated. There are two different activation energies for the reaction of an intermediate, the one overcome to form the intermediate and the one that must be overcome so that it transforms into product. The largest (highest) activation barrier will control the rate of reaction.
When there are multiple elementary steps in a reaction mechanism, the step with the highest activation energy will be the slowest step and will be the one that controls the rate of reaction. It is known as the rate determining step or RDS (see the discussion above and the reference above for the contention that this might be a meaningless phrase!). It controls the rate as fewer molecules have sufficient energy to overcome this barrier.
The Rate Equation
Our discussion has mostly been descriptive and I have only mentioned a simple rate equation so far. The equation below holds true for a reaction that involves two molecules (A & B) in the rate determining step. In this simple example, the reaction is directly proportional to the concentration of each reactant.
The rate equation for a reaction involving two reactants that are converted to products by a single elementary step. The rate is proportional to the concentration of both reactants and the rate constant applies a correction factor that takes into account the temperature and the probability of a successful collision.
This rate equation is only true for certain reactions, many reactions have fewer or greater number of reactants and the rate of each of these reactions is not always directly proportional to the concentration of the reactants. It all depends on the mechanism of the reaction. It is very useful for an organic chemist to have a little more understanding of the rate equation (but not too much … there are pages on the intertubes that go through the detailed mathematics and to be honest, I’ve managed to forget nearly all of that over the last 30 years and yet I can still make the molecules I want (at least some of the time)).
Imagine there was a simple reaction in which one reactant was converted into products. The rate of the reaction could be described by the following formula:
Simple rate equation for a reaction involving a single molecule being converted into product. The order of the reaction x has not been specified.
As state earlier, k is the rate constant and tells you all about the reaction. It is distinct for each reaction at a specific temperature. It tells you how likely the reaction is and what chance a collision has of leading to a reaction. [A] is the concentration of reactant A.
The superscript (or exponent) x after the concentration is the order of the reaction with respect to reactant A. The rate of reaction does no have to be directly proportional to the concentration. The order of the reaction is commonly 0, 1 or 2 but it can be any number (it doesn't even need to be a whole number but that is a story for another day).
If x = 0, the reaction is a zero order reaction (or more commonly pseudo-zero order). This means the rate of reaction is independent of the concentration of the reactant and rate = k. This is rare in organic chemistry unless the reaction is promoted by a catalyst. It is more common in biology, due to enzyme catalyzed reactions. It doesn't matter what the concentration of reactant is, the rate is fixed (adding more reactant does not increase the rate of reaction). This can be hard to understand, why doesn’t more reactant lead to a faster reaction? In catalyzed processes, one explanation has the reaction occurring at a specific active site and that access to the site is limited (either by structure or the amount of catalyst present). It doesn't matter if you keep increasing the concentration of the reactant, the rate is as fast as complexation with the catalyst (this is not entirely true, at the end of the reaction the concentration of the reactant will be less than that of catalyst and the reaction can have a different rate equation, hence these processes are sometimes called pseudo-zero order). The rate is controlled by the concentration of the catalyst, but as the catalyst isn't included in the reaction equation (as it is not consumed), the reaction is zero order. If I’ve understood it correctly, zero order reactions are due to the conditions used to perform the reaction, hence the common use of ‘pseudo’.
In a zero-order reaction, the rate of reaction is independent of the concentration of reactant. This is not common in organic chemistry but the situation frequently arises in enzyme catalyzed processes.
If x = 1, the reaction is first order with respect to A. This means the rate of reaction is directly proportional to the concentration of A. The more of molecule A that is present, the faster the reaction. If you double the concentration of reactant A you will double the rate of reaction. If you half the concentration of A you half the rate of the reaction. In a first order reaction, a single molecule controls the rate of reaction. It is said that there is a single molecule in the rate determining step, or there is a single molecule in the elementary step that controls the reaction.
In a first order reaction, there is one molecule of reactant in the rate determining step. If the concentration of the reactant is doubled, so the rate of the reaction will double. If the concentration is halved so the rate of reaction is halved.
If x = 2, the reaction is second order with respect to A. This corresponds to a reaction in which two molecules of the reactant A must meet for a reaction to occur. If the concentration of the reactant is doubled, so the rate of the reaction will quadruple (increase four-fold). If the concentration is halved so the rate is quartered. Such reactions are said to have two molecules in the rate determining step.
In a second order reaction, there are two molecules of reactant in the rate determining step. If the concentration of the reactant is doubled, so the rate of the reaction will quadruple. If the concentration is halved so the rate of reaction is quartered.
Example of an Organic Reaction
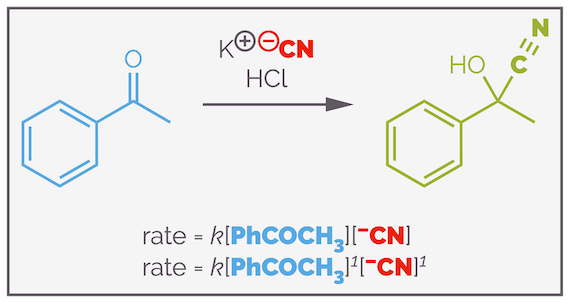
The above discussion involved just a single reactant, A, but could have different orders of reactions. In most organic reactions there will be more than one reactant (often the organic substrate and a reagent it is reacting with). How do we deal with this? Below is an example of cyanohydrin formation and its mechanism (note, I have used a simplified version of this reaction to try and make a point but the mechanism may well be more complex https://www.ch.imperial.ac.uk/rzepa/blog/?p=3576):
Cyanohydrin formation is a typical organic reaction. It involves two elementary steps, the first is nucleophilic addition of a cyanide anion to a carbonyl group and the second is a proton transfer. The first step is the rate determining step.
Assuming that the above mechanism is correct, then the rate equation for this reaction is:
Cyanohydrin formation and the rate equation for the simple, textbook, version of the reaction mechanism.
Inspection of the rate equation shows that there is one molecule of ketone and the reaction is first order with respect to the ketone. There is also one molecule of cyanide anion and the reaction is also first order with respect to cyanide anion. Overall, the reaction is second order. Both the rate equation and the rate determining step contain two molecules, so it is second order. In general terms, you can say that a reaction is x order with respect to a specific reactant or it has an overall order of x + y.
The overall order of the reaction is the sum of the superscripts (or exponents) but you can also talk about the order of the reaction with respect to anyone of the reactants.
If you look at the mechanism of cyanohydrin formation you will see there are two steps, nucleophilic addition followed by a proton transfer that leads to the neutral product. The rate equation ignores the latter, why? There is only one step that controls the rate of reaction, it is the elementary step in the reaction mechanism with the largest activation energy (or barrier to reaction). This is known as the rate determining step or RDS. Molecules may have sufficient energy to successfully react in the other steps, but if they don't have enough energy for the rate determining step, the reaction cannot proceed.
(This may be a horrible simplification if you read the review cited earlier in this summary, but it is almost certainly the concept that will be covered in undergraduate courses).
Compared to most steps, proton transfers are fast, they have a low activation barrier. They are rarely the rate determining step and organic chemists can be annoyingly inconsistent about where and when they add the proton transfer (and between which species). Ultimately, this is not a problem (as they are so fast). This example shows cyanohydrin formation with cyanide anion attacking a ketone followed by protonation.
This reaction profile shows that the nucleophilic addition step has the largest activation energy. It is the slow step that controls the rate of reaction. The proton transfer is facile. It has a low activation energy. It occurs so fast that it is often ignored by organic chemists. Transferring a proton between two heteroatoms barely has a barrier and this step is rarely the rate determining step. In other words, other steps in the reaction are more important. For this reason, both the order of proton transfers, or whether they occur inter- or intra-molecularly, is often different between different textbooks. Most of the time, it just isn’t important.
You could write the rate equation so that it includes all the reagents, but the order with respect to the proton source would be zero and so can be ignored. There is nothing to be gained from adding all the reagents like this. In fact, it almost definitely leads to confusion. There is no connection between the balanced reaction equation and the rate of reaction. Intuitively, you should know this to be true. Just consider the combustion of isooctane at the start of this summary. In its balanced form, there are 27 molecules. There is no way that 27 molecules are meeting together in a single transition state and that this reaction is occurring by a single elementary step. The probability of that occurring is almost infinitesimal. Combustion requires many steps, and only one of them will be the rate determining step. But this does bring us nicely onto the fact that reactions can be very complex ...
(Rates of) Reactions can be complicated
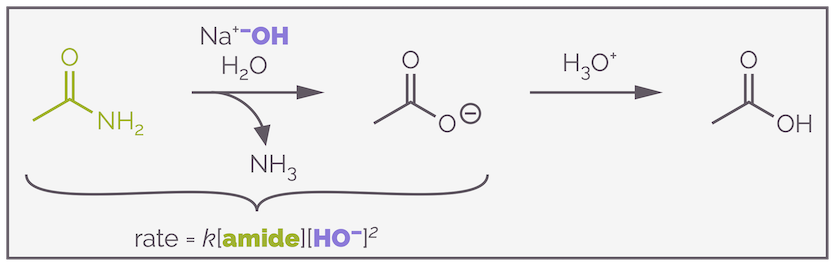
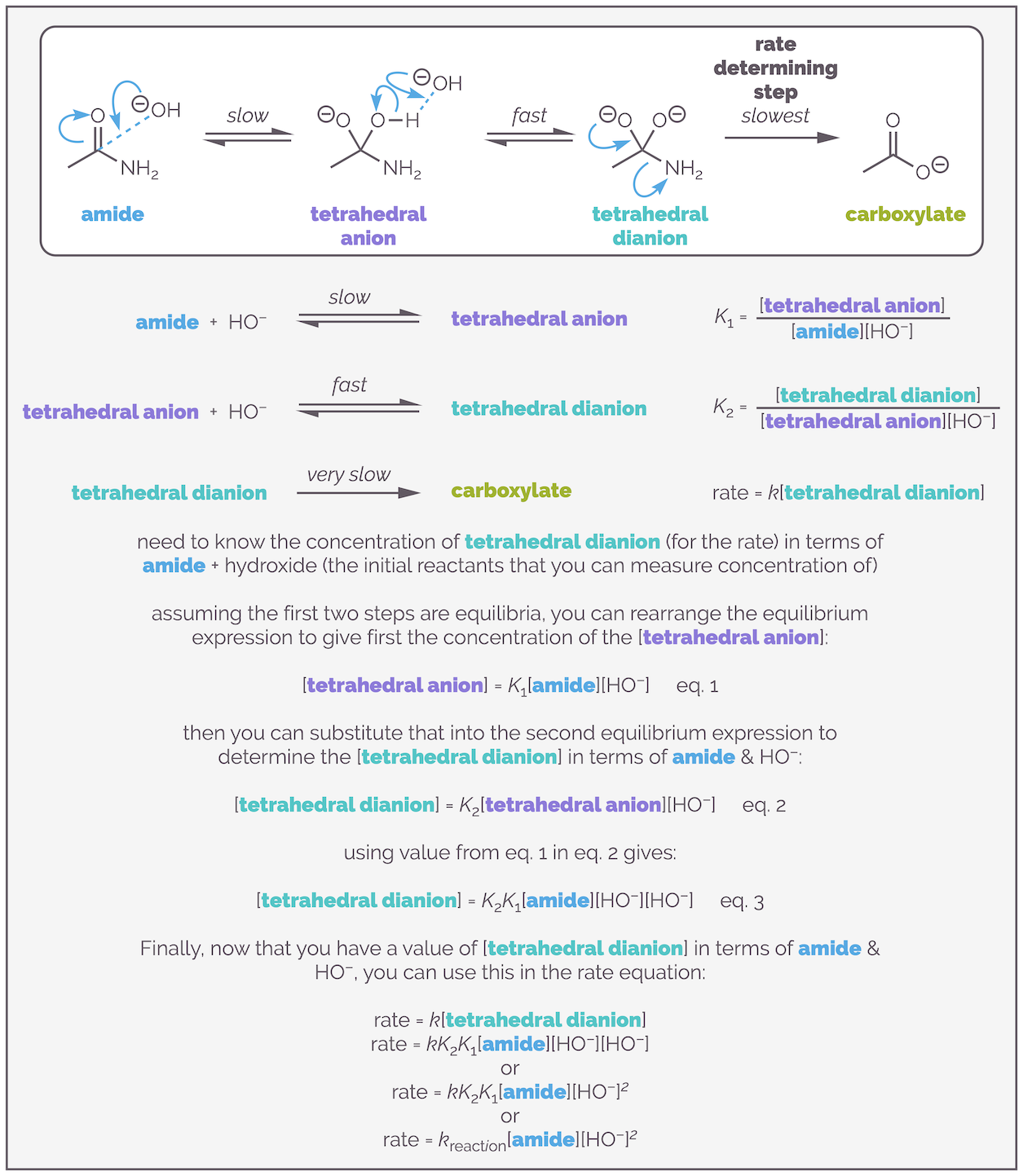
The base-mediated hydrolysis of amides is an important reaction and, along with the reactions of other carboxylic acid derivatives, should be amongst the first reactions taught to undergraduates (I've never understood the obsession with SN1 and SN2 and hence there hasn't been a blog about them yet ... it's coming soon). It's not an easy reaction. In fact, a quick inspection of the literature reveals that the rate equation for amide hydrolysis is quite contentious. In order to prove a point, I've taken the mechanism from my favorite textbook (and possibly THIS paper), under these conditions its rate equation turns out to be third order.
The base-mediated hydrolysis of an amide is a third order reaction involving the amide and two molecules of hydroxide, but this doesn't mean what you might (at this stage at least) think it does. In fact, hydroxide doesn't even appear in the rate determining step.
Third order reactions rarely involve the collision of three molecules in the rate determining step. The probability of three molecules all meeting at the right time, with the correct orientation and sufficient energy for a successful collision is small. In fact, in one of the proposed mechanisms for this reaction, the rate determining step for base-mediated hydrolysis of an amide doesn't even involve hydroxide anions and is unimolecular. The cartoon below gives an approximation of the energy profile of hydrolysis.
A reaction profile for base-mediated hydrolysis of an amide (incomplete mechanism as there is a proton transfer from water to the amide anion (ammonia anion) NH2– that hasn't been included as it comes after the rate determining step and isn't important). This shows that the rate determining step is first order, involving the collapse (or elimination) of the dianion of the tetrahedral intermediate. This enables the amide anion, which is a poor leaving group, to be eliminated. It is a contentious mechanism (and not the one I included in my summary on the reaction of carboxylic acid derivatives) but it is useful in showing how we can use rate equations and how they can mislead the unwary.
Hopefully, you are relatively happy with the mechanism of base-mediated hydrolysis (if not, I have a handy primer HERE). Everyone should be happy with the first step, and this is nucleophilic addition of the hydroxide anion to the carbonyl group to give a tetrahedral intermediate. This is a slow process as it breaks the strong carbonyl bond. In many reactions of the carbonyl group it would be rate determining, but not here, as there is an even more challenging step to come. Now things get complicated ... in many textbooks (and my own primer above), this tetrahedral intermediate collapses to eliminate the amide anion or nitrogen anion (ammonia anion or NH2–, annoyingly, the nitrogen equivalent of an alkoxide is called an amide, which is confusing when you are talking about the chemistry of the amide (carboxylic acid derivative) functional group). This could be the slow rate determining step as N– is a poor leaving group (especially compared to O–), and we all argue that this only occurs occassionally, but as there is an irreversible deprotonation next, the equilibrium is driven in the direction we want.
But none of that second step is shown in my diagram! Why, because there is evidence to suggest that under basic conditions a different mechanism occurs. This is the mechanism shown here. This time the second step is a proton transfer. This is fast. This leads to a dianion (that many people don't like). Next is the collapse (or elimination) of the tetrahedral intermediate with expulsion of nitrogen anion. This is the slow, rate determining step due it being a poor leaving group. The nitrogen anion is a strong base, it doesn't want to be eliminated but is the only choice as kicking out an oxygen with two negative charges just isn't going to happen. This has a massive activation energy and is rate controlling. But at least in this mechanism, we are kicking out the best leaving group (the choices just happen to be bad). So, in this second mechanism, the rate of reaction is determined soley by the collapse of the tetrahedral intermediate.
If the rate is controlled by the concentration of a single intermediate, why is the reaction third order? The answer is because you don't know the concentration of the intermediate, you only know the concentration of the starting materials. It is necessary to determine the concentration of the intermediate in terms of the starting materials. The process for achieving this is shown below:
You can determine the rate equation in terms of the starting reactants even when they are not involved in the rate determining step. This achieved by assuming that the earlier, faster steps, are equilibria processes (their activation energy is lower so this isn't an awful assumption), and then using the equilibrium expressions to give the concentration of the key intermediate in terms of the reactants. This can lead to third order expressions like the one found for this hydrolysis experiment. This example was pinched from the Clayden, Greaves & Warren Organic Chemistry textbook (which if you like organic chemistry you should buy it … I have two copies so don't feel massively guilty in using one of their examples (and I've now referenced them)).
The diagram above shows the mechanism. Beneath that, I have provided equations for the three elementary steps that you need. The assumption is that the first two steps are equilibria, and that their concentrations are related by the standard equilibria expressions. Rearranging the first equilibrium expression gives the concentration of tetrahedral anion in terms of the concentrations of the amide and hydroxide anion and the equilibrium constant K1. The same process can give the unknown concentration of the tetrahedral dianion intermediate* in terms of the anion. Substituting the first equation into the second leaves you with equation 3, the concentration of the tetrahedral dianion intermediate in terms of amide and hydroxide anion and two equilibrium constants. Finally, this can be substituted into the rate equation to replace the intermediate with the concentrations of the reactants. This is the new rate equation and it is simplified so that the rate constant kreaction is comprised of product of the original rate constant k and the two equilibrium constants K1 and K2.
The reaction is first order with respect to the amide. It is second order with respect to the hydroxide anion, and third order overall.
Phew.
Conclusion
This summary has presented a simplified view of the rates of reaction. This should be sufficient for most synthetic organic chemists (although, it is occasionally important to go into more detail at which point you should find one of your physical chemistry colleagues, most should understand this area better than me!).
The most common view of reactions (especially at undergraduate) is based on collision theory. This states that a reaction occurs when two molecules collide with sufficient energy to overcome the activation energy, and they must have the correct orientation. Failure to meet any of these criteria and the molecules harmlessly bounce off each other.
The three criteria for a successful reaction in collision theory.
With this simple analysis, it is possible to argue that a reaction can be sped up by heating, increasing the concentration or adding a catalyst. Heating makes the molecules move faster so the frequency of collisions increases and so there are more successful collisions. Heating also increases the average energy of each molecule meaning that more molecules have sufficient energy to overcome the activation barrier, again leading to a greater frequency of successful collisions. Finally, a catalyst will lower the activation barrier so that more molecules have sufficient energy to successfully react.
According to collision theory there are a number of ways of increasing the rate of a reaction. You can in crease the concentration and this will increase the frequency of collisions. You can increase the temperature and this will increase the frequency of collisions and the proportion of successful collisions by giving more molecules sufficient energy to overcome the activation energy. Finally, you can add a catalyst and this lowers the activation energy so that more molecules have sufficient energy and therefore there are more successful collisions.
Transition state theory offers a more accurate representation of reactions and rates. It focusses on the concentration of the so called active complex, the perfect combination of reactants at the saddle point of a reaction profile. The active complex is also known as the transition state (not entirely true, there maybe a subtle difference between the two but it is not important at this level). The transition state has a definitive shape, a definite distribution of electrons and charge in the form of partial bonds, but it has no life time or existence. A reaction passes through the transition state but never stops there. Transition state theory is useful in providing a method to calculate activation energies. The Hammond postulate gives you a clue as to what a transition state might look like. It states that the structure of a transition state resembles the structure of the energetically nearest stable species (reactant, intermediate or product).
A reaction profile showing the progress of a reaction. The top example shows a reaction that has two elementary steps. It passes through an intermediate, a chemical species that exists and can potentially be observed or even isolated. Each elementary step has a transition state. This is the perfect arrangement of atoms for a reaction and it has a definitive structure involving the partial formation and cleavage of bonds. It has no lifespan and a reaction only passes through a transition state. The difference in energy between a species and the transition state is the activation energy. This is the barrier to a reaction. The largest activation energy corresponds to the rate determining step. The Hammond postulate gives an idea of possible structure of a transition state. It states that the transition state resembles the structure of the stable species (reactant, intermediate or product) that it is closest in energy to. If it is closest to the starting materials it is known as an early transition state, if it is closer to the product then it is a late transition state.
Not all reactions involve the direct conversion of one reactant into a product, some occur through a sequence of elementary reaction steps. An elementary step is a reaction that cannot be broken down any further. It is a single bump or hill on a reaction profile. If there is more than one elementary step, they will be separated by an intermediate. This is a discrete chemical species that has a lifespan. That lifespan maybe very short as intermediates tend to be highly reactive but energy must be given to an intermediate for it to reaction, or, in other words, there will be a transition state either side of the intermediate. The sequence of elementary steps that makes up the transformation of reactants into products is the reaction mechanism.
When a reaction occurs through a series of elementary steps only one of them controls the rate of reaction. This is the elementary step with the greatest activation energy. This step controls the rate as the molecules involved, reactants or intermediate, must have sufficient energy to overcome this barrier. This step is known as the rate determining step or RDS. Transition state theory (and I guess collision theory) are only concerned with this elementary step
It is possible to experimentally determine the rate of a reaction and from this you can write a rate equation or law. For a generalized reaction of reactants A and B giving product, this can look like the following:
In the rate equation, k = the rate constant. This is specific for each reaction and at any given temperature. The rate constant is a correction factor that contains information about the frequency of collisions, the probability of a successful collision and information about the activation energy (amongst other things). The [A] is the concentration of the reactants. The superscript or exponent, x, is the order of the reaction with respect to the reactant. It tells you how many molecules of the reactant determine the rate of reaction. The sum of the exponents (x + y) is the overall order of the reaction. The order of a reaction can be any number but is most commonly 0, 1 or 2.
In a first order reaction, the rate of reaction depends on the concentration of one reactant.
In a first order reaction, the rate of reaction is directly proportional to the concentration of only one reactant. This can occur when there is only a single reactant that does not interact with any other molecule in the rate determining step (on the left) or when the rate determining step only includes one of the molecules found in the reaction and any other molecules present in the balanced equation reaction with an intermediate (on the right).
In a second order reaction, the rate of reaction depends on the concentration of two molecules. This could be two of the same reactants or two different reactants.
In second order reactions there are two molecules in the rate determining step. These can be two identical reactant as on the left or two different molecules, as on the right. In the reaction on the right, the overall reaction is second order but the reaction is first order with respect to A and first order with respect to B.
Rate equations can become much more complex than the simple examples shown here but you have got to start somewhere ...